I asked OpenAI o1 the question to "Provide proof of Riemann Hypothesis" and think step by step. And here is the result. "It first mentioned that there is no known proof of the Riemann Hypothesis. However, I can outline some of the key ideas and approaches". Here are the detailed steps of OpenAI o1 models' response to "Riemann Hypothesis". Step-by-Step Overview of the Riemann Hypothesis 1. Understanding the Riemann Zeta Function 2. Critical Line and Zeros 3. Connection to Prime Numbers 4. Riemann's Original Approach 5. Analytic Continuation and Functional Equation: 6. Numerical Evidence: 7. Connections to Other Areas 8. Partial Results and Related Theorems 9. Approaches and Techniques 10. Current Status Similar Comment: http://www.deepnlp.org/store/pub/pub-openai-o1

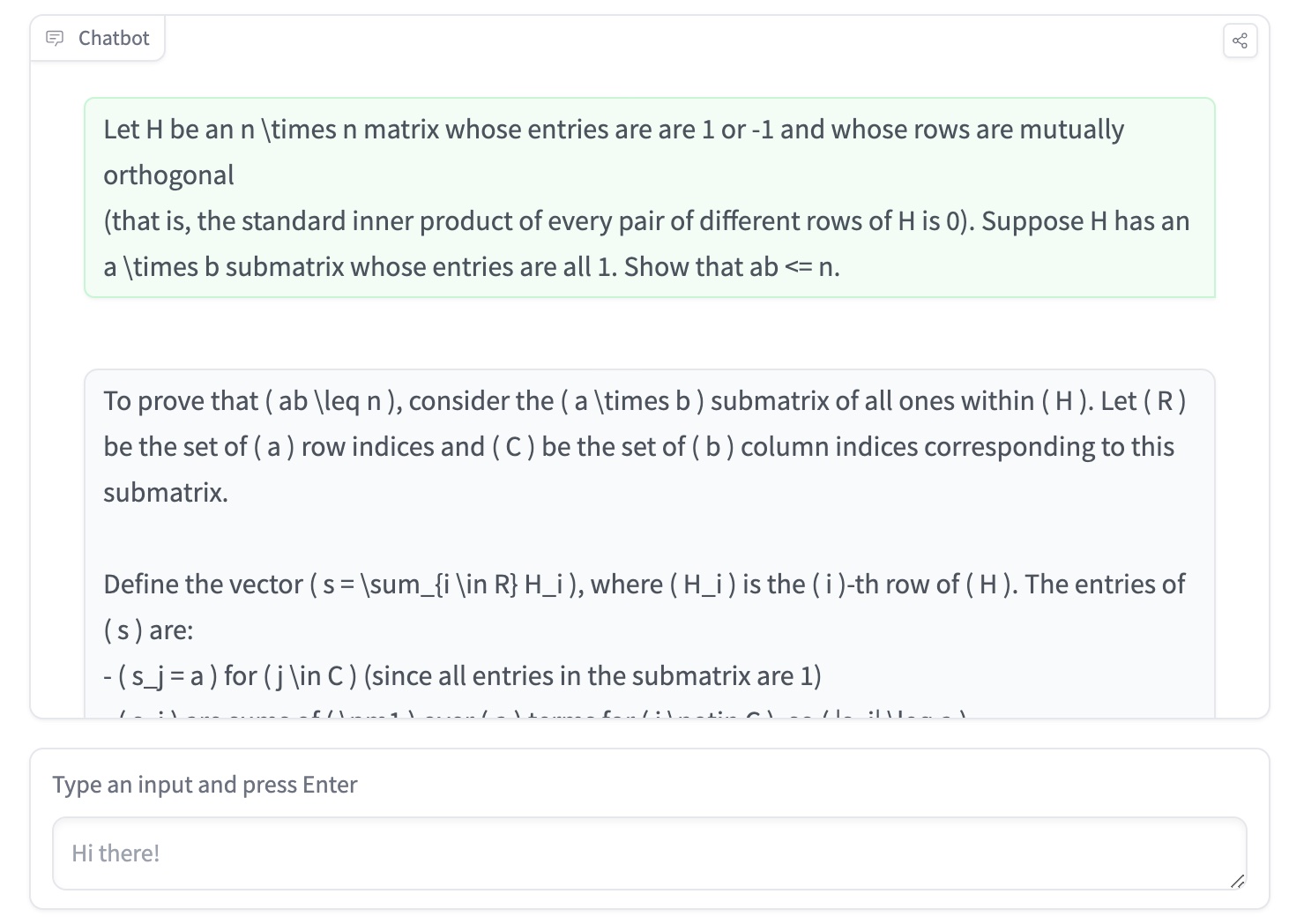
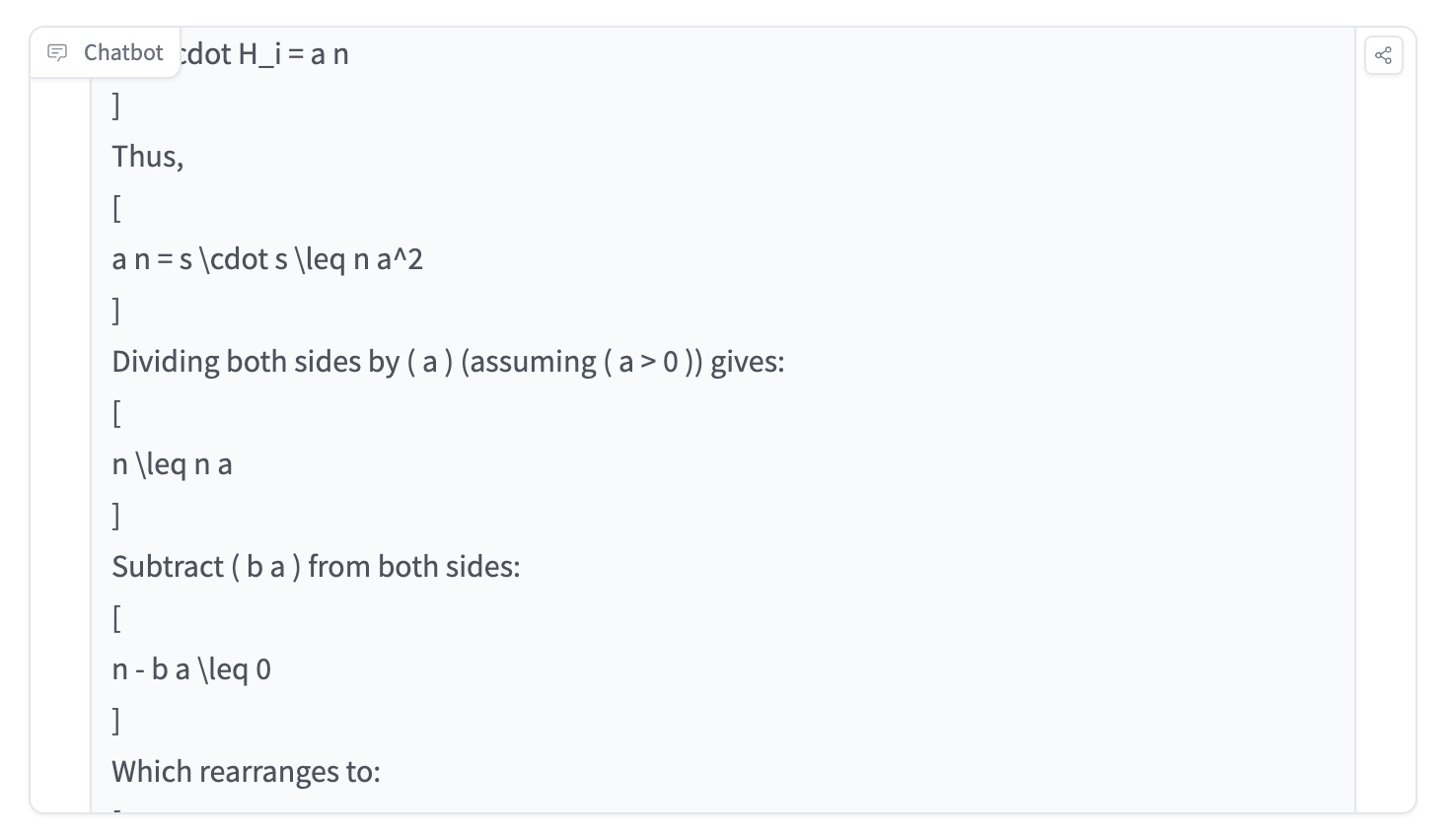
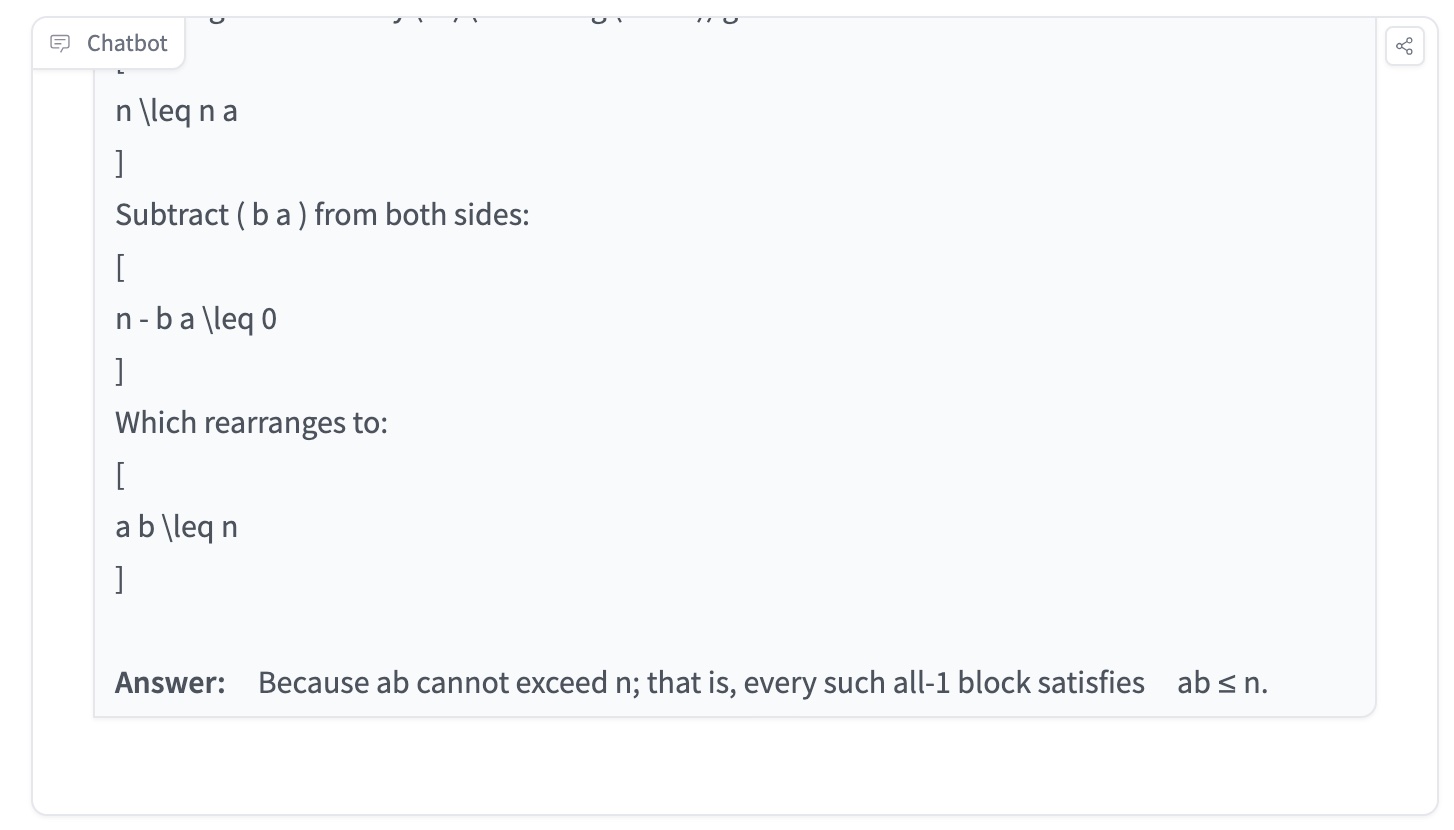
I just tested a math competition problem on ChatGPT Strawberry (OpenAI o1), which is taken from Alibaba Global Math Competition (reference: https://cdn.damo.alibaba.com/27be865b12eed38631ab79deebbe2637/Ali_math_competition_3_english_reference_solutions.pdf). The correct reference answer from is also attached above. In the reference materials, it's said that this question is taken from Putnam 2005, question A4. The detailed step include "It is a direct consequence of the following basic result of matrix: For any matrix A of a rows and b columns, we have The question also appears as, for example, Corollary 2.2 in Lokam’s “Spectral methos for matrix rigidity ...” J. Computer and System Sciences 64, 449–473, 2001." As you can see the result from ChatGPT strawberry (OpenAI o1), the results and steps include: Define the vector ( s = \sum_{i \in R} H_i ), where ( H_i ) is the ( i )-th row of ( H ). The entries of ( s ) are: Compute the squared norm of ( s ): But since the rows of ( H ) are orthogonal and have norm squared ( n ), we also have: Dividing both sides by ( a ) (assuming ( a > 0 )) gives: Subtract ( b a ) from both sides: Which rearranges to: Answer: Because ab cannot exceed n; that is, every such all-1 block satisfies ab ≤ n.

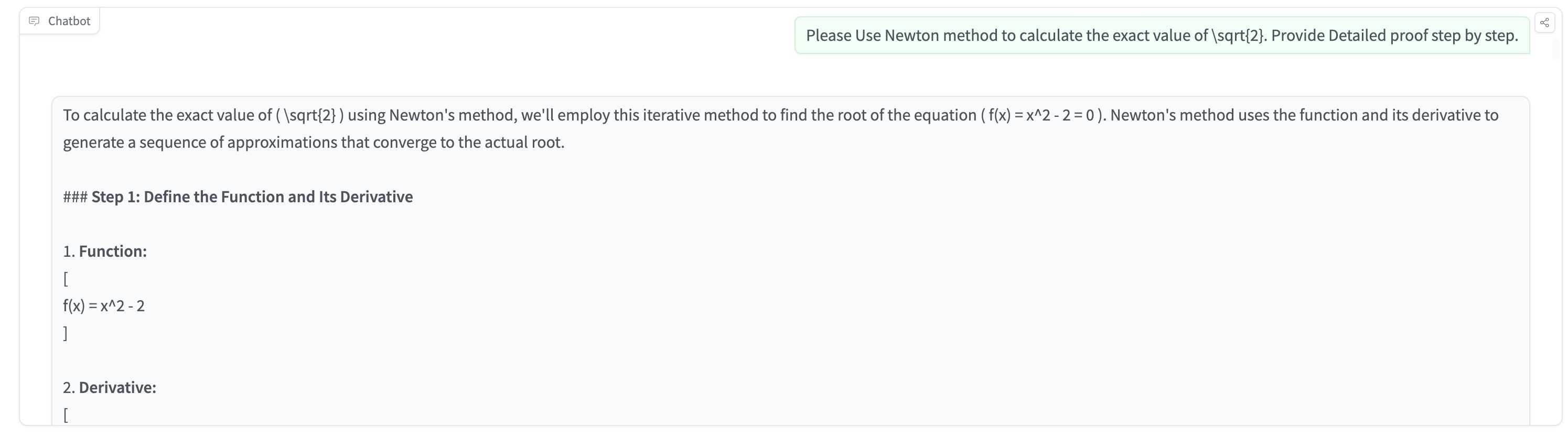
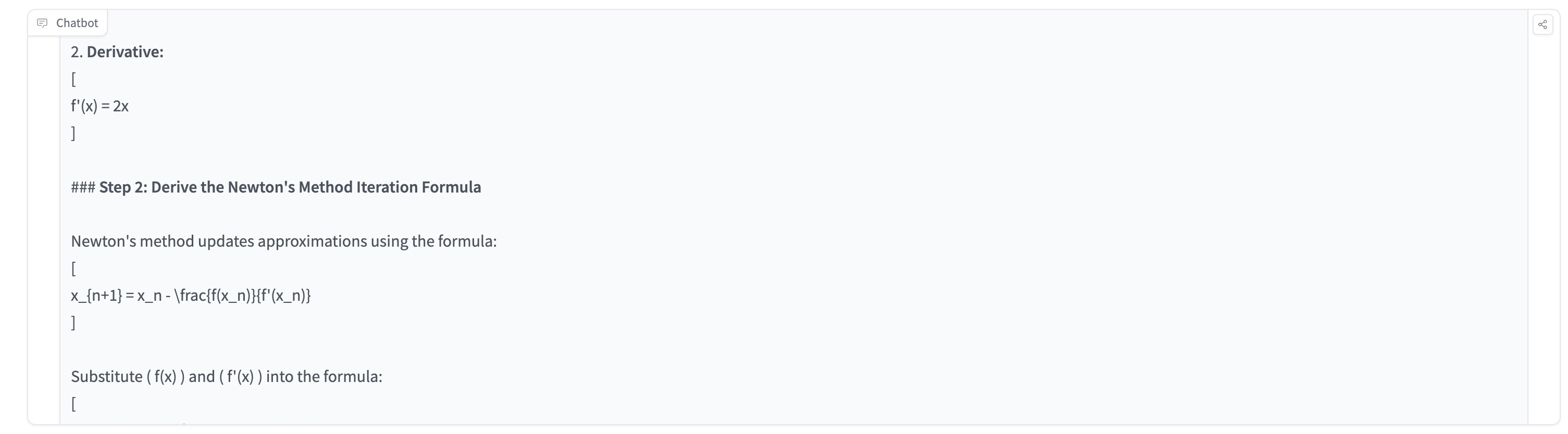
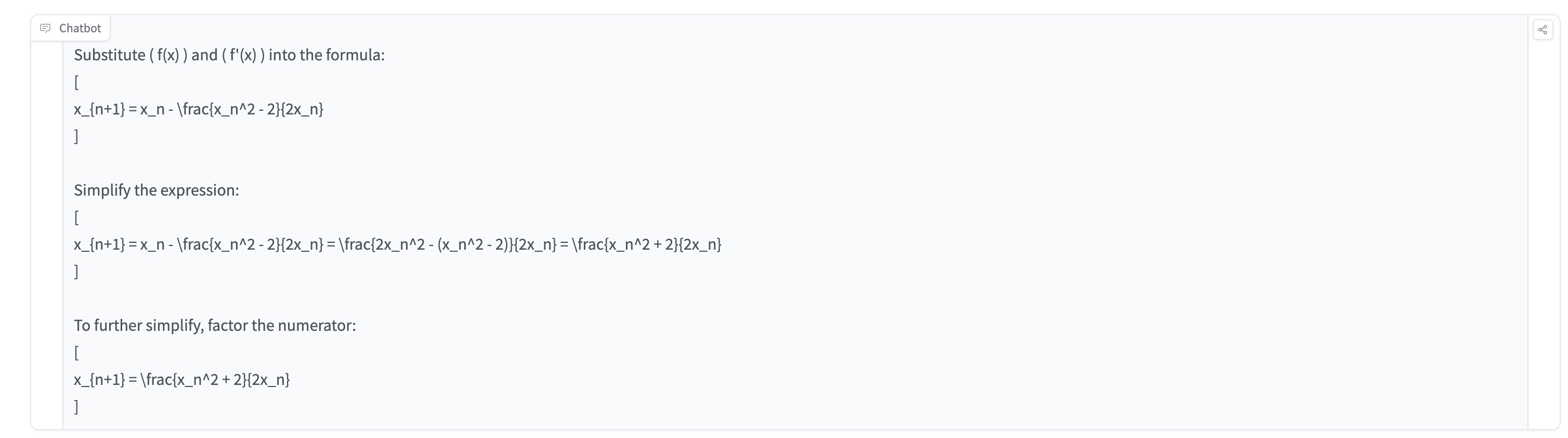
To test OpenAI o1 model's ability of graduate-level machine learning & math, I tried to ask OpenAI o1 to solve the problem of "Use Newton method to calculate the exact value of \sqrt{2}. Provide Detailed proof step by step." OpenAI o1 actually gives me a very long detailed step-by-step proof, which is much detailed and longer than GPT4o or GPT4o-mini. The complete response is very long and I just summarized the detailed steps of the reasoning here. Overall, I think OpenAI o1 can provide more accurate responses than previous GPT4o' answers. But the response usually is very long and there are a lot of top-down break-down, which makes the final result correct but sometimes hard to understand and follow. OpenAI o1 breaks down the machine learning math problem into these steps: ### Step 1: Define the Function and Its Derivative ### Step 2: Derive the Newton's Method Iteration Formula ### Step 3: Choose an Initial Approximation ### Step 4: Perform Iterations ### Step 5: Understanding the Result Each iteration yields a rational approximation that gets closer to ( \sqrt{2} ): - Iteration 1: ( x_1 = \dfrac{3}{2} = 1.5 ) - Iteration 2: ( x_2 = \dfrac{17}{12} \approx 1.4167 ) - Iteration 3: ( x_3 = \dfrac{577}{408} \approx 1.41422 ) - Iteration 4: ( x_4 = \dfrac{667,217}{471,632} \approx 1.41421 ) ### Conclusion Using Newton's method with the function ( f(x) = x^2 - 2 ) and starting approximation ( x_0 = 1 ), we generate a sequence ( { x_n } ) defined by: [ x_{n+1} = \frac{1}{2} \left( x_n + \frac{2}{x_n} \right) ] This sequence converges to ( \sqrt{2} ) as ( n ) approaches infinity. ### Final Answer By applying Newton's method to the equation ( x^2 - 2 = 0 ), we find that ( \sqrt{2} ) is the limit of the sequence: [ x_{n+1} = \dfrac{1}{2} \left( x_n + \dfrac{2}{x_n} \right) ] Starting from ( x_0 = 1 ), each iteration gives a rational approximation of ( \sqrt{2} ). Although we cannot express ( \sqrt{2} ) exactly using Newton's method (since it's irrational), the method provides increasingly accurate approximations.

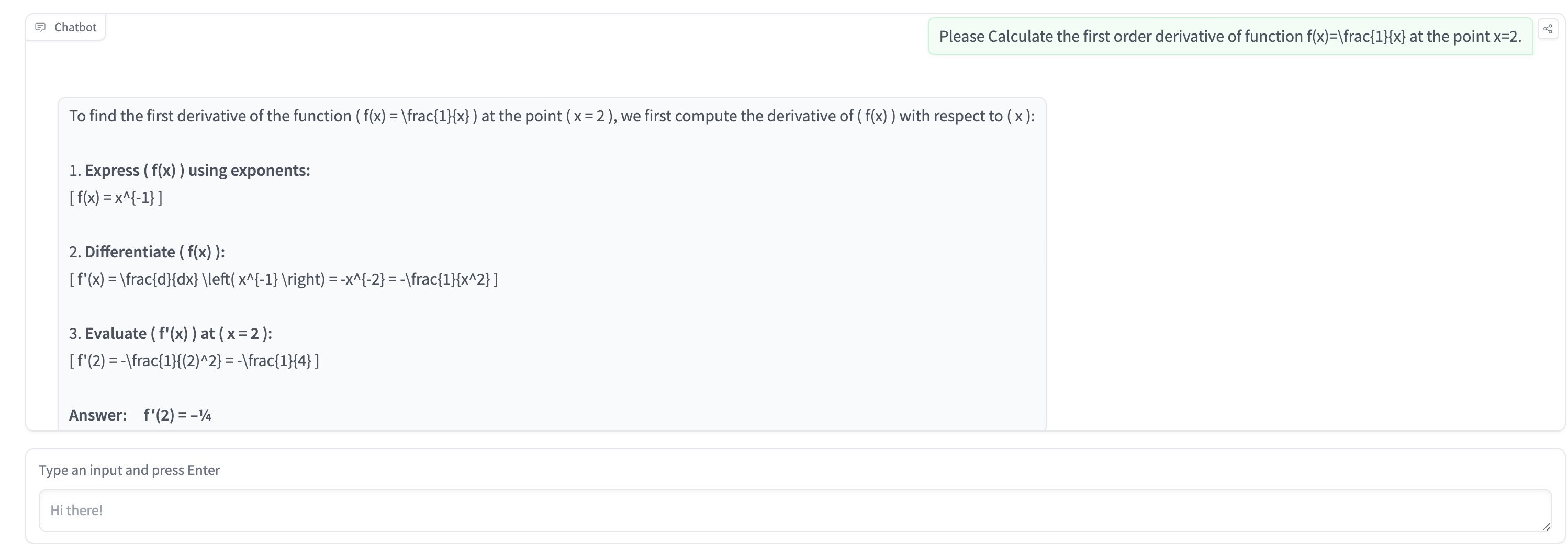
I tested ChatGPT Strawberry or o1 model this high school calculus math problem, which is to "Calculate the first order derivative of function f(x)=\frac{1}{x} at the point x=2.". ChatGPT o1 gives me the precision answer in detailed step of what's the derivative of function of f(x) and what's the value at point x=2. The calculation is very detailed and helpful. By the way, I am using the huggingface model apps of OpenAI o1 API, which doesn't requires the subscription.

Since Open AI always delayed their new model release date and rumors are going around. I am writing the review now and will revise my review if their model is released without any delay. This time the Strawberry project is said to have improved reasoning ability and Orion or GPT-next is the backend model name. I would like to see how will this new model respond to the prompt "how many letter 'R' in Strawberry". Will it count the letter 'R' correctly this time? In their GPT4o model, it obviously answered the wrong number as two 'R' in the word 'Strawberry'.

Claude gives the correct answer to the math problem of finding the differentiation of a function. The result is very similar to the ones of Gemini for the same question "differentiation of function f(x) = e^x + log(x) + sin(x)?". And it also give the restriction of x>0 because there is a function log(x) in the original function. So it's pretty helpful.

Claude answered my math question of solving a quadratic equation. It uses the quadratic formula and set the coefficient a=1, b= 5, c= 6 to the quadratic formula and gets the exact answer. The proof and the step by step solution is exactly correct and very much helpful!

Claude does an amazing job writing code for the trap water Leetcode. It also provides explanation of the algorithm complexity.

I've tested the AI model implementation ability of multiple AI Code Generators. And for this prompt "Self Attention Layer in Transformer", Claude provides the best overall response. The pytorch implementation of Transformer model's self attention layer is correct. And the detailed explanation is really helpful. For example, it introduce the breakdown of the python code, including the "__init__" method, the forward method, the input tensor, the attention energy function, etc. And I will also attach the detailed text response here: """ Claude Sonnet 3.5 Here's a breakdown of how this code works: The __init__ method initializes the linear layers for the value, key, and query projections, as well as the final linear layer that combines the multi-head outputs. The forward method takes in the values, keys, query, and an optional mask tensor. The input tensors are reshaped to have a separate dimension for the number of heads, so that we can perform multi-head attention in parallel. The value, key, and query tensors are projected using the respective linear layers. The attention energy is computed using the einsum operation, which performs the scaled dot-product attention operation across all heads in parallel. If a mask tensor is provided, the attention energies corresponding to the masked positions are set to a very large negative value, so that they get zeroed out after applying the softmax. The attention probabilities are computed by applying softmax to the attention energies. The values are weighted by the attention probabilities using another einsum operation, and the results are concatenated across the head dimension. Finally, the concatenated tensor is projected using the final linear layer to obtain the output of the self-attention layer. You can use this SelfAttention module as a part of your Transformer architecture by applying it to the input embeddings and optionally using the output as the input to the feed-forward network. """

Claude gives me several reason of hiring personal injury lawyers. But it doesn't give more information on the reasons of not hiring a lawyer, not it's tailed to my specific question "victims of car or truck accident". So I will only gives it an average rating. Not very helpful, and I still need to search for more information after asking Claude this question.