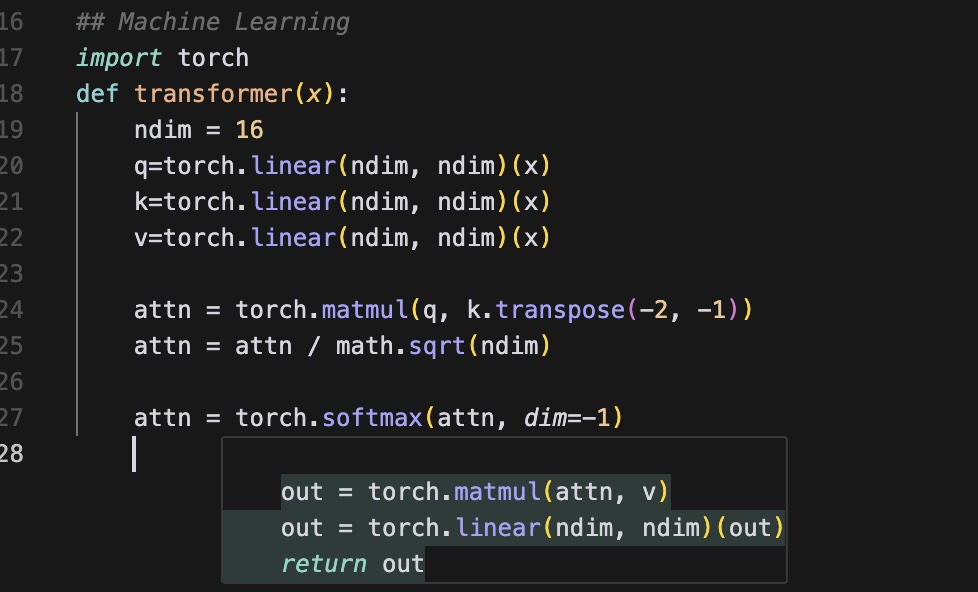
Another more complicated task I tested on Cursor Code Editor is to write a python code to implement the Transformer function as in paper "Attention is all you need". The code I am writing include function name "def transformer(x):" and some of the beginning lines like "q=torch.linear(". And with the suggested code, I wrap up the transformer function in less than one minutes. So it can really help me increase the productivity of writing code. The only drawback is when I want to modify the code and use backspace to delete some lines, it seems like Cursor doesn't know what to do and give no hints for a while. Unless I start writing something else. And the newly suggested code will usually be quite different from the previously suggested ones. ``` ## Machine Learning ### Input import torch def transformer(x): ndim = 16 q=torch.linear(ndim, ndim)(x) k=torch.linear(ndim, ndim)(x) v=torch.linear(ndim, ndim)(x) attn = torch.matmul(q, k.transpose(-2, -1)) attn = attn / math.sqrt(ndim) attn = torch.softmax(attn, dim=-1) ### Cursor Suggested Code: out = torch.matmul(attn, v) out = torch.linear(ndim, ndim)(out) return out ```

I asked Gemini to solve this graduate-level machine learning math problem "Use Newton method to calculate the exact value of \sqrt{2}. Provide Detailed proof step by step". And Gemini provides correct and concise answers to this question. It breaks down into a few steps: 1. Initial Guess, which is to Let's start with an initial guess, say x 0=1. This is a reasonable guess since 1^2 is close to 2. 2. Newton's Method Formula 3. Iterations 4. Convergence and get the conclusion Newton's method converges quadratically, which means that the number of correct digits approximately doubles with each iteration. As we continue iterating, we'll get closer and closer to the exact value of \sqrt{2}.

Gemini provides the correct answer to my high-school level math question about calculus "Calculate the first order derivative of function f(x)=\frac{1}{x} at the point x=2.". It uses the power rule to get the derivative function f'(x) and calculate its value at point x=2. And gets the correct answer -1/4. The answer is helpful, concise and easy to understand.

Gemini gives the correct answer of the math problem of calculating differentiation of function. It applies the step by step thinking and firstly outlines the method it uses to solve the differentiation "use the sum rule and the derivatives of individual functions". Then it gives detailed proof as follows: To find the derivative of f(x) = e^x + log(x) + sin(x), we'll use the sum rule and the derivatives of individual functions. The sum rule states that the derivative of a sum of functions is the sum of the derivatives of the individual functions.   Here are the derivatives of the individual functions: Derivative of e^x: d/dx(e^x) = e^x Derivative of log(x): d/dx(log(x)) = 1/x Derivative of sin(x): d/dx(sin(x)) = cos(x) Applying the sum rule, we get: f'(x) = d/dx(e^x) + d/dx(log(x)) + d/dx(sin(x)) f'(x) = e^x + 1/x + cos(x) Therefore, the derivative of f(x) = e^x + log(x) + sin(x) is f'(x) = e^x + 1/x + cos(x).

Gemini gives the correct answer to the quadratic equation x^2+5x+6=0 and it's using the step by step thinking method, which is very similar to the results from Claude, but different from the factoring methods of ChatGPT. Overall, the response from Gemini on solving this math problem is correct and helpful.