Compare
Overview
OpenAI o1 vs ChatGPT for image Comparison in different aspects of AI services with data mining from genuine user reviews & ratings, including: ALL,Interesting,Helpfulness,Correctness. AI store is a platform of genuine user reviews,rating and AI generated contents, covering a wide range of categories including AI Image Generators, AI Chatbot & Assistant, AI Productivity Tool, AI Video Generator, AI in Healthcare, AI in Education, AI in Lifestyle, AI in Finance, AI in Business, AI in Law, AI in Travel, AI in News, AI in Entertainment, AI for Kids, AI for Elderly, AI Search Engine, AI Quadruped Robot.
Reviews Comparison
Recommended Tags
-
xiaolei98 2024-09-13 12:16I used the OpenAI o1 preview model to implement the frontend code of login and logout function of H5 mobile application and separate css, html and js code into separate files. The model's response to the front end code generation task is very helpful. And I actually copy and paste the code into a separate folder and tried it myself. The website front end is shown in the attached images. It is working to some extend, except that the CSS file is a little bit strange. The o1 model generates the code and also gives these explanations, including: index.html: Contains the structure of the login and logout pages. styles.css: Provides the styling for the pages to make them mobile-friendly. scripts.js: Handles the login and logout functionality. It uses localStorage to persist the logged-in state.


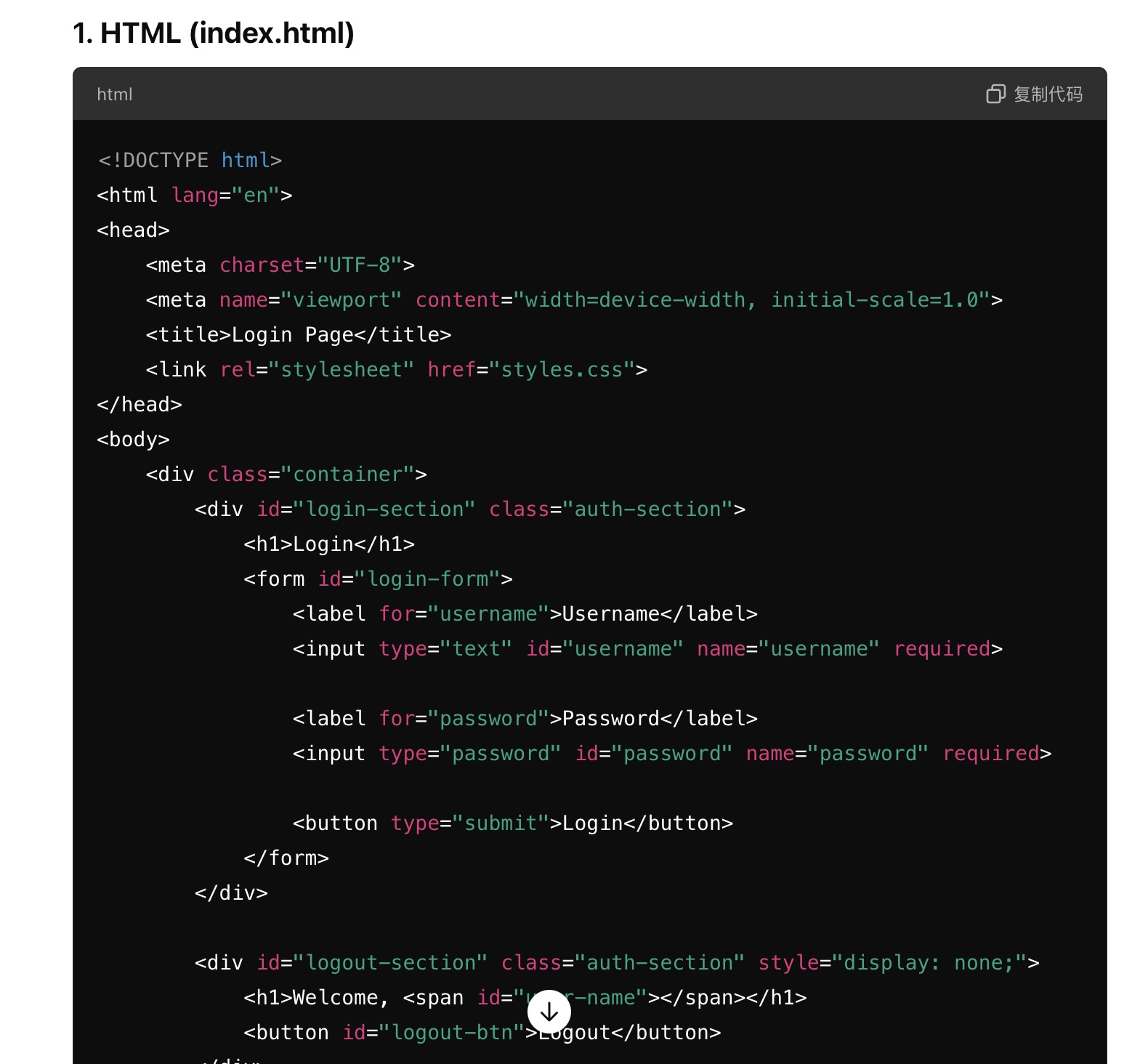
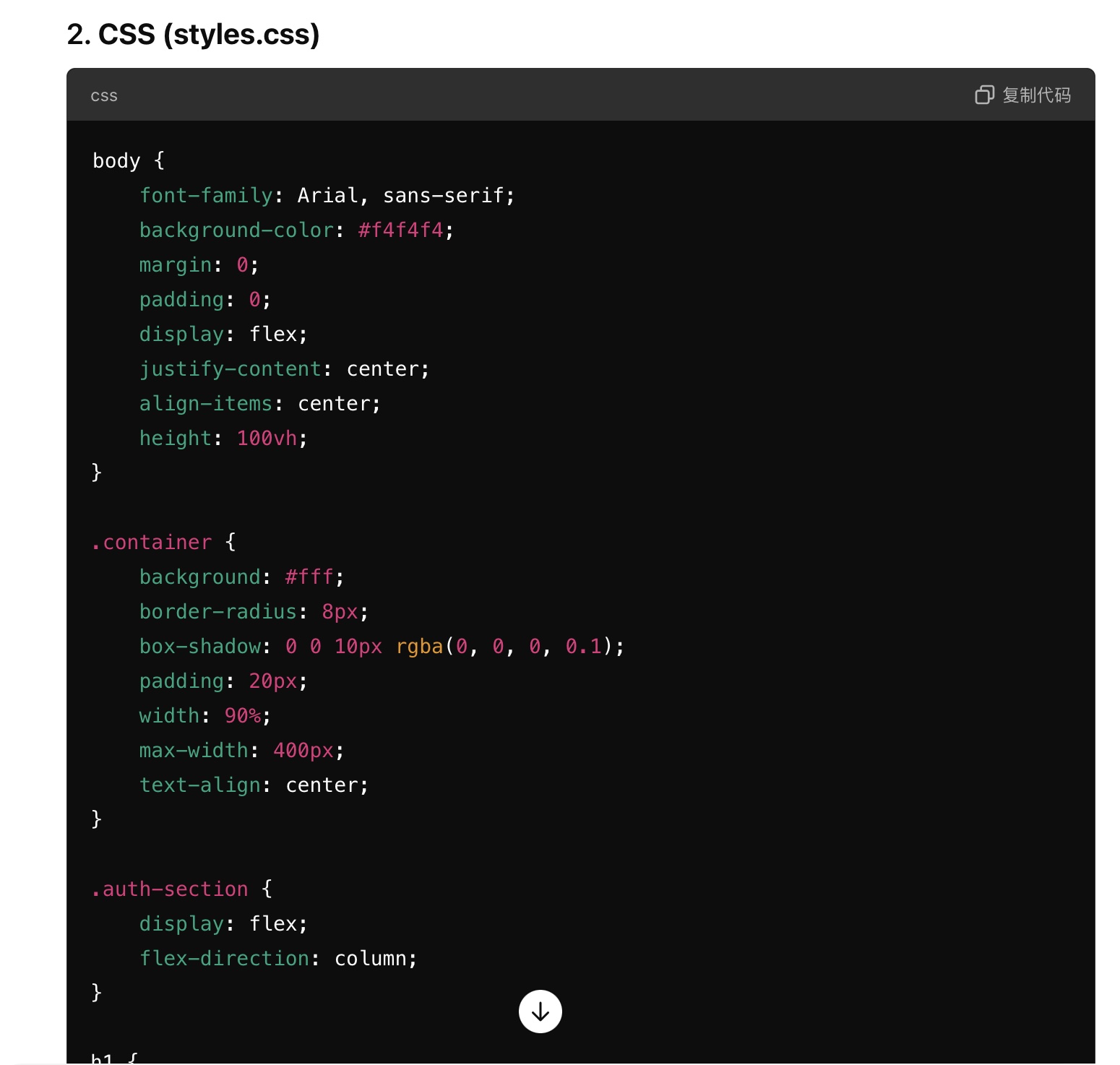
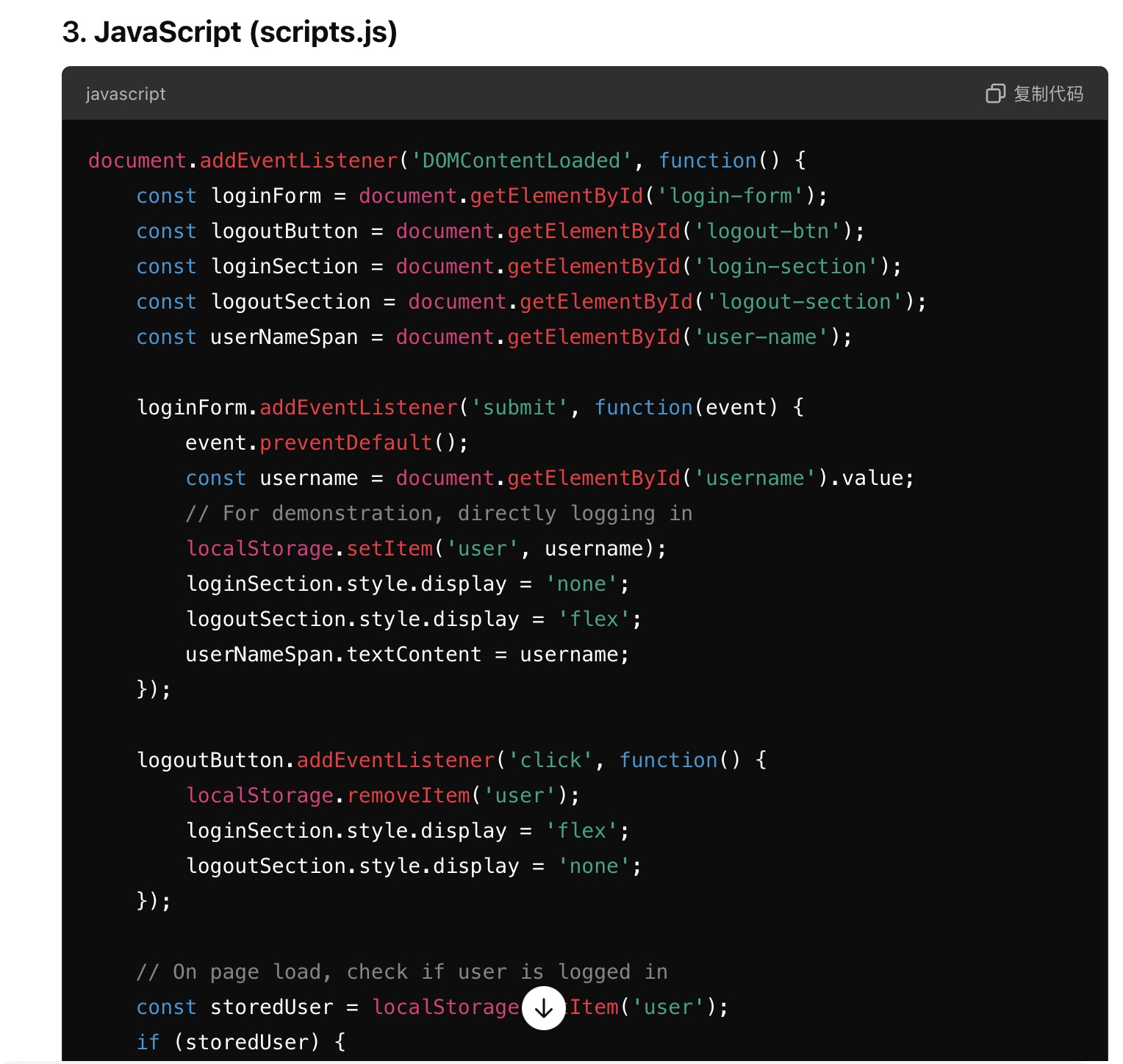
-
kai 2025-03-29 10:19ChatGPT GPT4o generation produced interesting pictures. This cartoon style images are amazing

-
ai4science03 2024-09-09 12:38Truthfully, I am a little bit surprised by the math proof ability and reasoning ability of ChatGPT. To solve the topological math problem, ChatGPT firstly gives a outline of the proof and provides more details to support the proof. The detailed response is as follows: To prove that the sum of two compact sets in a topological vector space X, X is compact, we need to show that if A and B are compact subsets of X, then A+B is also compact. Proof: 1. Recall Definitions and Properties 2. Consider the Projection Maps 3. Use the Compactness of A and B 4. Image of a Compact Set Under a Continuous Map 5. Conclusion: Thus, we have shown that if A and B are compact subsets of a topological vector space X, then A+B is also compact.

-
Community
-
Please leave your thoughts on the best and coolest AI Generated Images.
-
Please leave your thoughts on free alternatives to Midjourney Stable Diffusion and other AI Image Generators.
-
Please leave your thoughs on the most scary or creepiest AI Generated Images.
-
We are witnessing great success in recent development of generative Artificial Intelligence in many fields, such as AI assistant, Chatbot, AI Writer. Among all the AI native products, AI Search Engine such as Perplexity, Gemini and SearchGPT are most attrative to website owners, bloggers and web content publishers. AI Search Engine is a new tool to provide answers directly to users' questions (queries). In this blog, we will give some brief introduction to basic concepts of AI Search Engine, including Large Language Models (LLM), Retrieval-Augmented Generation(RAG), Citations and Sources. Then we will highlight some majors differences between traditional Search Engine Optimization (SEO) and Generative Engine Optimization(GEO). And then we will cover some latest research and strategies to help website owners or content publishers to better optimize their content in Generative AI Search Engines.
-
We are seeing more applications of robotaxi and self-driving vehicles worldwide. Many large companies such as Waymo, Tesla and Baidu are accelerating their speed of robotaxi deployment in multiple cities. Some human drivers especially cab drivers worry that they will lose their jobs due to AI. They argue that the lower operating cost and AI can work technically 24 hours a day without any rest like human will have more competing advantage than humans. What do you think?
-
Please leave your thoughts on whether human artists will be replaced by AI Image Generator. Some similar posts on other platforms including quora and reddit. Is art even worth making anymore, Will AI art eventually permanently replace human artists, Do you think AI will ever replace artists, Do people really think that replacing artists with ai is a good idea


Reply