To test OpenAI o1 model's ability of graduate-level machine learning & math, I tried to ask OpenAI o1 to solve the problem of "Use Newton method to calculate the exact value of \sqrt{2}. Provide Detailed proof step by step." OpenAI o1 actually gives me a very long detailed step-by-step proof, which is much detailed and longer than GPT4o or GPT4o-mini. The complete response is very long and I just summarized the detailed steps of the reasoning here. Overall, I think OpenAI o1 can provide more accurate responses than previous GPT4o' answers. But the response usually is very long and there are a lot of top-down break-down, which makes the final result correct but sometimes hard to understand and follow. OpenAI o1 breaks down the machine learning math problem into these steps: ### Step 1: Define the Function and Its Derivative ### Step 2: Derive the Newton's Method Iteration Formula ### Step 3: Choose an Initial Approximation ### Step 4: Perform Iterations ### Step 5: Understanding the Result Each iteration yields a rational approximation that gets closer to ( \sqrt{2} ): - Iteration 1: ( x_1 = \dfrac{3}{2} = 1.5 ) - Iteration 2: ( x_2 = \dfrac{17}{12} \approx 1.4167 ) - Iteration 3: ( x_3 = \dfrac{577}{408} \approx 1.41422 ) - Iteration 4: ( x_4 = \dfrac{667,217}{471,632} \approx 1.41421 ) ### Conclusion Using Newton's method with the function ( f(x) = x^2 - 2 ) and starting approximation ( x_0 = 1 ), we generate a sequence ( { x_n } ) defined by: [ x_{n+1} = \frac{1}{2} \left( x_n + \frac{2}{x_n} \right) ] This sequence converges to ( \sqrt{2} ) as ( n ) approaches infinity. ### Final Answer By applying Newton's method to the equation ( x^2 - 2 = 0 ), we find that ( \sqrt{2} ) is the limit of the sequence: [ x_{n+1} = \dfrac{1}{2} \left( x_n + \dfrac{2}{x_n} \right) ] Starting from ( x_0 = 1 ), each iteration gives a rational approximation of ( \sqrt{2} ). Although we cannot express ( \sqrt{2} ) exactly using Newton's method (since it's irrational), the method provides increasingly accurate approximations.

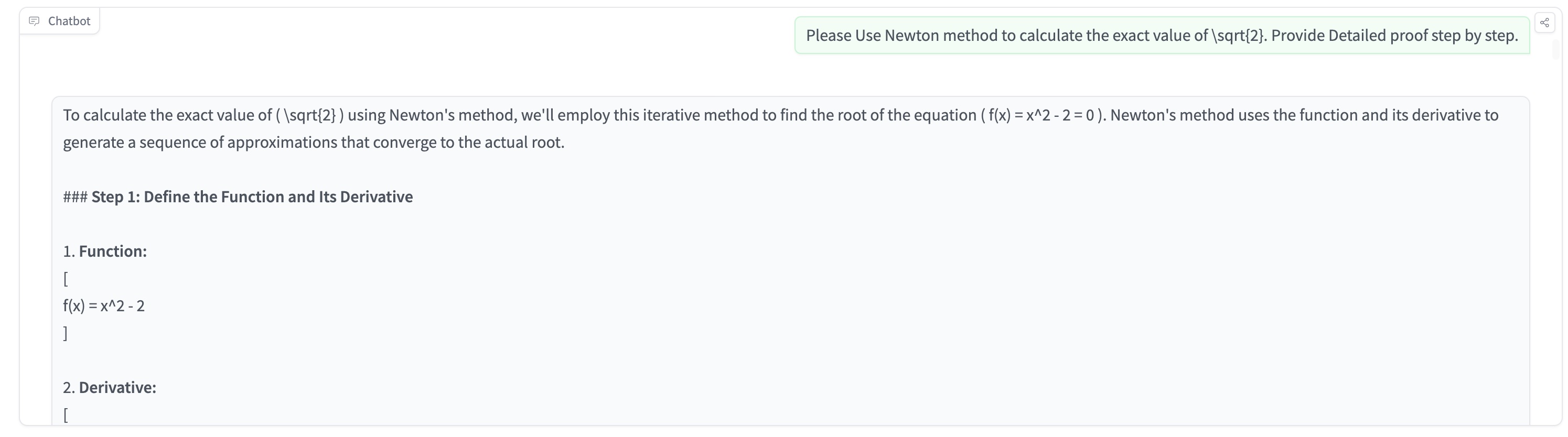
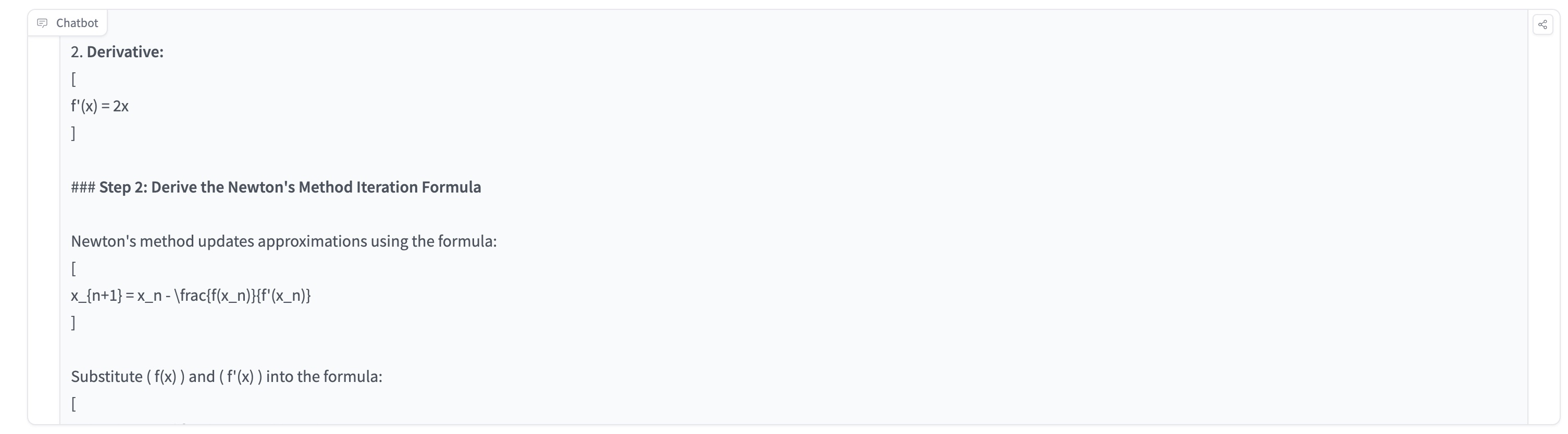
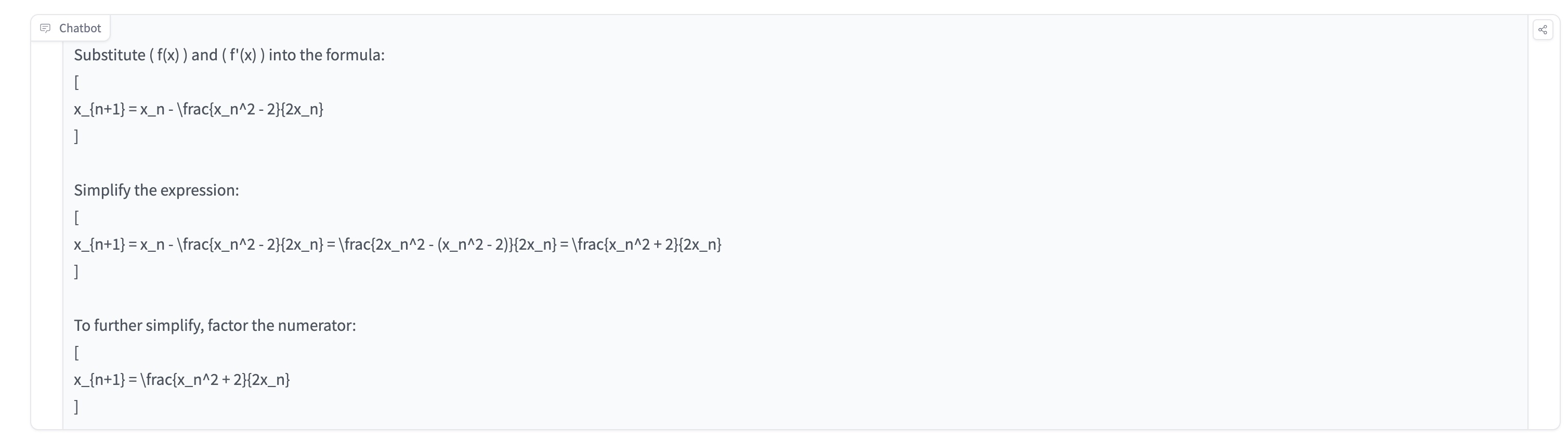
Finally, OpenAI released o1 mdoel with stronger reasoning ability. And I looked through the detailed comparison of a math solving results on their website and the comparison between GPT4o vs OpenAI o1-preview on this Algebra problem. For the math question as the in the prompt, o1 uses a chain of thought when attempting to solve a problem, which is similar to how a human may think for a long time before responding to a difficult question. o1 response actually break down the question into a few steps: "Understanding the Given Information", "Defining a New Polynomial", "Properties of q(x)", "Constructing s(x)", "Matching Coefficients". Finding Additional Solutions and finally reaching Conclusion. The additional real numbers x satisfying p(1/x) = x^{2} are x=\frac{1}{n!} or -\frac{1}{n!}. Overall, the reasoning ability is quite complex compared to previous version, so it's helpful and the answers are correct.

I asked Gemini to solve this graduate-level machine learning math problem "Use Newton method to calculate the exact value of \sqrt{2}. Provide Detailed proof step by step". And Gemini provides correct and concise answers to this question. It breaks down into a few steps: 1. Initial Guess, which is to Let's start with an initial guess, say x 0=1. This is a reasonable guess since 1^2 is close to 2. 2. Newton's Method Formula 3. Iterations 4. Convergence and get the conclusion Newton's method converges quadratically, which means that the number of correct digits approximately doubles with each iteration. As we continue iterating, we'll get closer and closer to the exact value of \sqrt{2}.

Gemini provides the correct answer to my high-school level math question about calculus "Calculate the first order derivative of function f(x)=\frac{1}{x} at the point x=2.". It uses the power rule to get the derivative function f'(x) and calculate its value at point x=2. And gets the correct answer -1/4. The answer is helpful, concise and easy to understand.

Gemini gives the correct answer of the math problem of calculating differentiation of function. It applies the step by step thinking and firstly outlines the method it uses to solve the differentiation "use the sum rule and the derivatives of individual functions". Then it gives detailed proof as follows: To find the derivative of f(x) = e^x + log(x) + sin(x), we'll use the sum rule and the derivatives of individual functions. The sum rule states that the derivative of a sum of functions is the sum of the derivatives of the individual functions.   Here are the derivatives of the individual functions: Derivative of e^x: d/dx(e^x) = e^x Derivative of log(x): d/dx(log(x)) = 1/x Derivative of sin(x): d/dx(sin(x)) = cos(x) Applying the sum rule, we get: f'(x) = d/dx(e^x) + d/dx(log(x)) + d/dx(sin(x)) f'(x) = e^x + 1/x + cos(x) Therefore, the derivative of f(x) = e^x + log(x) + sin(x) is f'(x) = e^x + 1/x + cos(x).

Gemini gives the correct answer to the quadratic equation x^2+5x+6=0 and it's using the step by step thinking method, which is very similar to the results from Claude, but different from the factoring methods of ChatGPT. Overall, the response from Gemini on solving this math problem is correct and helpful.