DeepSeek V3 has very high hallucination compared to other large MoE model with such huge size of parameters.

There is not public access to test the prover model. And I tried to use a previous prompt in machine learning to ask DeepSeek model to make a proof. But it seems like the question is over simplified and it only gave some introductory summarization. But the thinking process is quite interesting.

The deepseek company loves to release new models before festival holidays. The May Labor holiday is approaching and there are high probabilities that new model R2 will be released. I am quite excited to this release and see how OpenAI is going to respond.

I asked DeepSeek R1 model to to calculate the exact value of \sqrt{2} using Newton method, which is a classic Machine Learning Task. The results from DeepSeek R1 model are pretty good. It even prints out the whole thinking process as part of the LLM output. The thinking took about 101 seconds. And I just listed a few point of the thinking process below: Okay, let's see. The user wants me to use the Newton method to calculate the exact value of sqrt(2). Hmm, Newton method, right? That's the Newton-Raphson method for finding roots. So, first, I need to recall how that works. The idea is to iteratively approach the root of a function by using the tangent line approximations. Alright, so sqrt(2) is the solution to the equation x^2 = 2. To apply Newton's method, I should reformulate this as a root-finding problem. That means defining a function f(x) such that f(x) = 0 when x is sqrt(2). So, let's set f(x) = x^2 - 2. The root of this function is indeed x = sqrt(2). Next, I remember the Newton-Raphson formula: x_{n+1} = x_n - f(x_n)/f'(x_n). I need to compute the derivative of f(x). The derivative f'(x) is 2x. Plugging that into the formula gives x_{n+1} = x_n - (x_n^2 - 2)/(2x_n). Let me simplify that expression. Starting with x_{n+1} = x_n - (x_n^2 - 2)/(2x_n). Let's split the fraction: (x_n^2 - 2)/(2x_n) = x_n/(2) - 1/x_n. Wait, no. Let me actually compute it step by step. Alternatively, maybe combine the terms. x_n - (x_n^2 - 2)/(2x_n) = (2x_n^2 - (x_n^2 - 2)) / (2x_n) = (2x_n^2 - x_n^2 + 2) / (2x_n) = (x_n^2 + 2) / (2x_n). Wait, that doesn't seem right. Wait, let's check the algebra again. Wait, x_{n+1} = x_n - (x_n^2 - 2)/(2x_n). Let's compute this as: x_{n+1} = x_n - (x_n^2)/(2x_n) + 2/(2x_n) = x_n - x_n/2 + 1/x_n = (x_n/2) + (1/x_n). So, simplifying, x_{n+1} = (x_n + 2/x_n)/2. Ah, that's the familiar formula for the square root using Newton's method. So each iteration averages x_n and 2/x_n. Okay, so now I need to choose an initial guess x_0. Since sqrt(2) is between 1 and 2, let's pick x_0 = 1.5 as a reasonable starting point. Wait, or maybe x_0 = 2? Let me think. The method usually converges regardless of the initial guess, but a better guess might converge faster. Let's try both and see. Wait, the user wants the exact value, but Newton's method gives an approximation. Wait, but sqrt(2) is irrational, so we can't get an exact value numerically, but perhaps they want to show the iterative steps converging to sqrt(2). But the exact value can't be computed exactly with Newton's method because it's an iterative approximation. So maybe the question is to show the steps until a certain precision is reached.

Great Efforts from DeepSeek which open sourced their R1 model. It's great challenge to OpenAI o1 and o3 reasoning models.

DeepSeek R1 models provides detailed thinking process of generating responses of complex math coding problems with surprisingly lower cost. The best part about deepseek is that they even open source their model. Great job done.

I tried to ask Perplexity the same question shown in SearchGPT demo "When can I see Nudibranchs in Half Moon Bay this weekend?" and "Will it be hot?". For the first question, Perplexity gave me an answer of the low tide time of Pillar Point specifically on "July 25, 2024" as "For Pillar Point in Half Moon Bay specifically, there is a good low tide opportunity this weekend: Thursday, July 25, 2024 at 8:18 AM with a low tide of -0.02 ft". And it also remind me of where to find the "Nudibranchs" as "To find nudibranchs, look carefully in tidepools and on seaweed". Pictures of Nudibranchs are also attached on the right panel of the search engine. Overall, it's really helpful and the information is realtime. Answer From Perplexity Based on the search results, you can see nudibranchs in Half Moon Bay this weekend during low tide periods. Here are the key details: The best time to see nudibranchs is during low tide when tidepools are exposed. For Pillar Point in Half Moon Bay specifically, there is a good low tide opportunity this weekend: Thursday, July 25, 2024 at 8:18 AM with a low tide of -0.02 ft It's recommended to arrive before the lowest tide time so you can explore the tidepools before the tide rises again. Pillar Point is known as an excellent location for seeing nudibranchs, with some areas referred to as "nudibranch pools" where they are particularly abundant. To find nudibranchs, look carefully in tidepools and on seaweed. Many species are small and require close observation to spot. Bring an underwater camera if possible, as nudibranchs can be colorful and photogenic. Be respectful of the marine environment - don't remove anything from the tidepools and watch your step to avoid damaging the habitat. Remember to check local tide tables for the most up-to-date information, as tide times can vary. Also, be aware of safety precautions like never turning your back on the ocean and wearing appropriate footwear for tidepooling.

Perplexity summarized 11 key factors of choosing pacemaker for elderly people from data sources including ncbi.nlm, etc. Overall the response is very helpful and informative.

Perplexity's answer to this personal injury question is pretty helpful. And I can also cite the web resources for further investigation. Perplexity acts as a personal injury lawyer and provides below advice, including "As a personal injury lawyer, I understand your concern about ensuring the insurance company doesn't take advantage of you during negotiations. Here are some key steps to protect yourself: Be cautious with statements, Document everything, Gather evidence, Understand your policy, Don't rush to settle, Be wary of early offers, Calculate full damages, Seek legal advice, Know your rights, Be prepared to negotiate and Keep emotions in check".

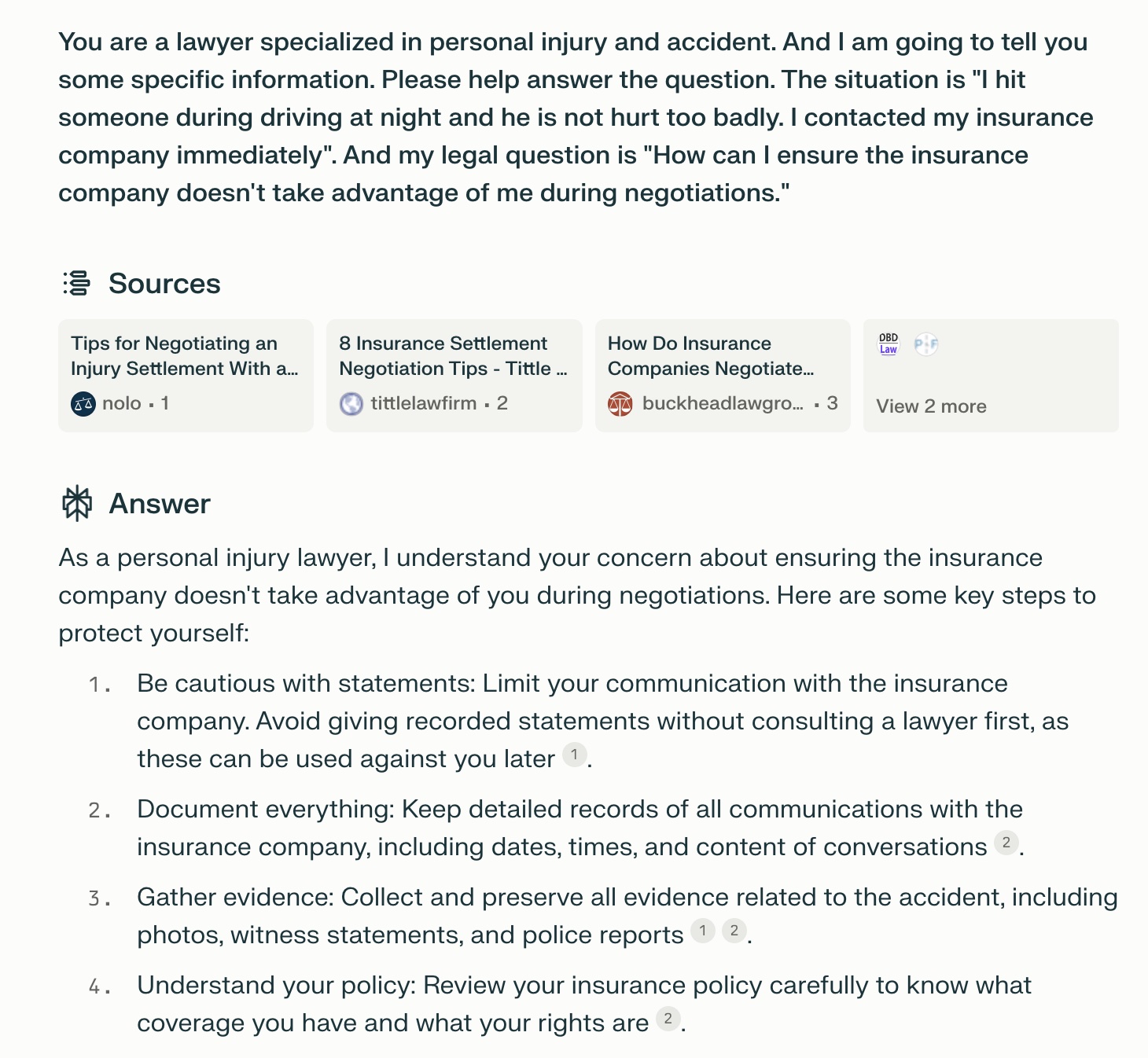
Perplexity summarizes the information related to "compensation for a pedestrian hit by a car" from several data sources and lists below factors to get compensation, including "Potential for compensation", "Modified comparative fault", "Determining fault", "Reduced compensation", "Insurance claim process", "Legal representation" and "Potential damages". So the respond is pretty helpful.

The results are trustworthy and helpful. Perplexity summarized the information from multiple data sources, and give replies to my question "how to cover my life expenses and get compensation from my ex-husband in New York?", which include "Spousal maintenance", "Temporary support" , "Equitable distribution", "Legal fees", "Seeking employment", "Public assistance" and "Free legal aid", etc. The data covers several sources, including "New York Temporary Alimony", "Help Centers & Community Organizations", "newyorkdivorceattorney.com".

Perplexity helps me lists a few steps to legally change my child's name. It also cite the websites from Forbes "How To Change A Child's Last Name Legally In 2024 - Forbes" and selfhelp.court "Change child's name both parents".

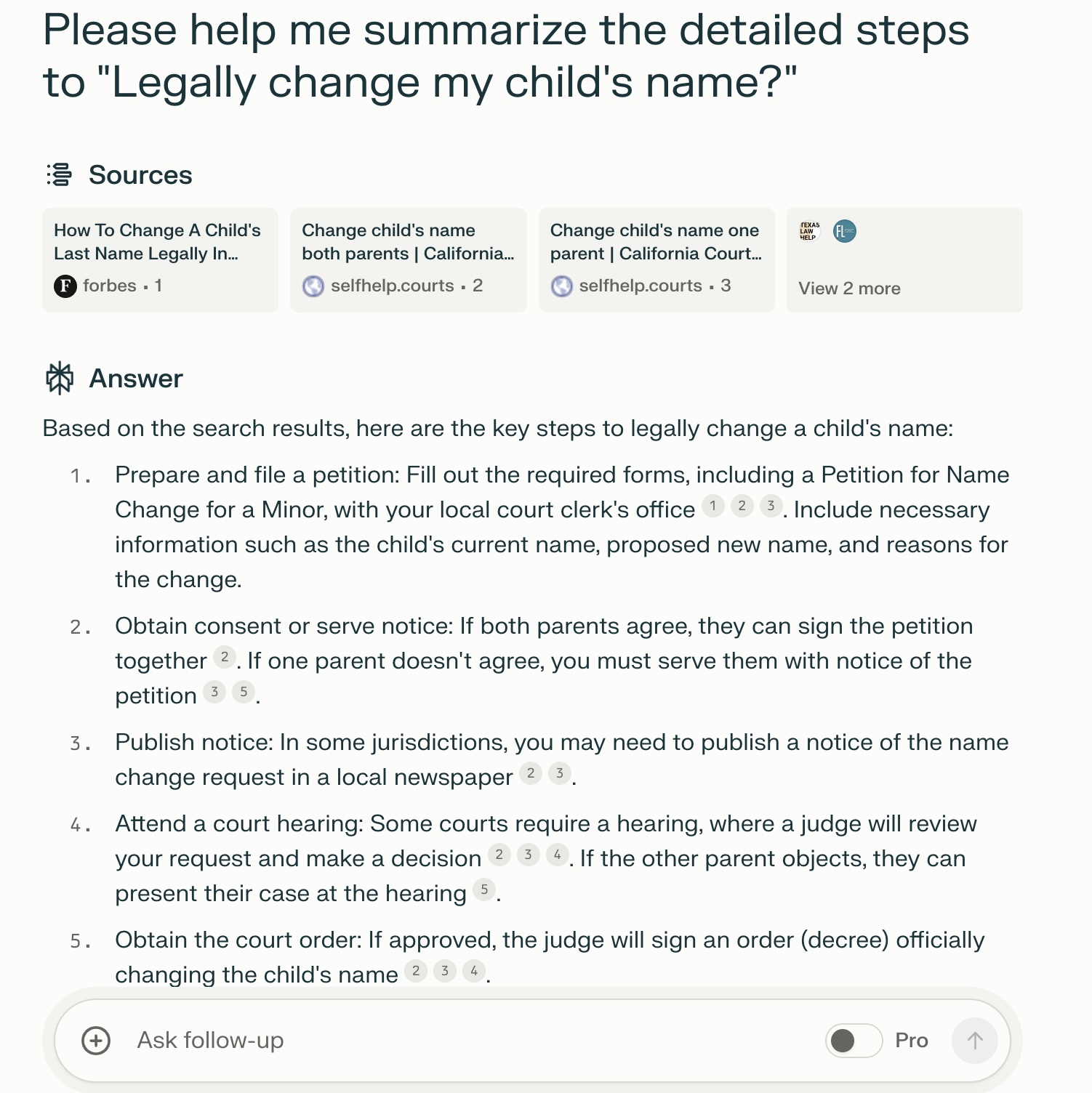
Perplexity provides really helpful responses to my question "What's are my rights to visit my children despite my ex-wife doesn't allow me to?". It mentioned 7 rights to visit my children despite the objection from my ex-wife, including "Court-ordered visitation rights", "Enforcement of visitation rights", "Modification of custody", "Police involvement", "Child's best interests", "Avoid self-help measures" and "Legal representation".

The answers from perplexity about child welfare and foster care is helpful but very limited. It discussed the situation regarding custody in case of divorce in general, possibility of foster care and living with grandparents. At the end it advises the questioner to speak with a trusted adult, school counselor, or local child welfare services for more specific guidance and support. Overall, the answer is correct but lacks of many important information, such as resources of websites or telephone number of trustworthy legal departments.

Perplexity answers my question "What factors to consider when choosing nursing homes for elderly people in San Jose" and provides 12 key factors to consider. In the end, it summarize "Remember to visit potential nursing homes multiple times, including unannounced visits, to get a comprehensive understanding of the facility's operations and atmosphere. Use tools like Medicare's Nursing Home Compare to gather additional information and compare different options in the San Jose area". Overall, I think this suggestion is really helpful. And perplexity did a good job finding the data source and made the automatic summary.

Perplexity does a good job summarizing NVIDIA's Q1 FY25 GAAP Financial Report Summary, and gives the number of Revenue: $26.0 billion up 18% quarter-over-quarter, Gross margin: 78.4%, up 2.4 percentage points from Q4, Operating income: $16.91 billion, up 24% from Q4 and 690%, Net income: $14.88 billion, up 21% from Q4. For the P/E ratio comparison, perplexity actually failed the job and gives a rough step of step method of how to calculate P/E ratio, but doesn't provides me an answer. For Google and Apple's P/E ratio, perplexity also replies that it is not provided in the search results. So I am not very satisfied with this results. Why can't it have access to some financial data, at least yesterday's archived data?

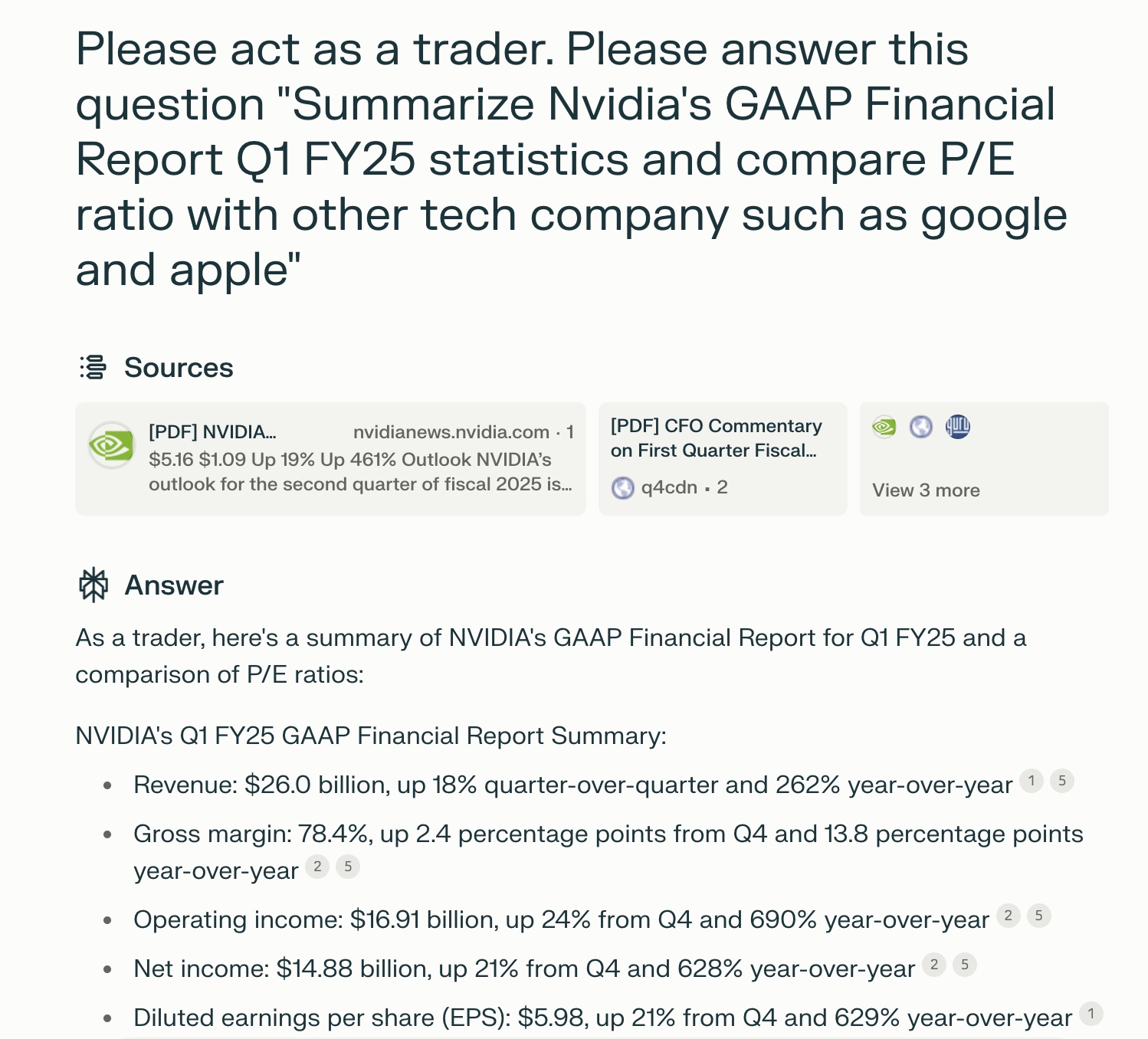
I asked some questions about "lip augmentation surgery" and perplexity helps me summarize the details from multiple data sources, including "clevelandclinic.org" and "webmd.com". And the responses are quite helpful. As for the second question "Can I get lip augmentation surgery at the age of 15?", perplexity gives 6 reasons not to perform lip augmentation surgery, including Age and development, Legal considerations, FDA guidelines, Psychological factors, Medical ethics and Alternative options. Prompt: 1. You are an expert in plastic surgery and I will ask you a few question about beauty in healthcare. The first question is "What is a lip augmentation surgery and are the lip fillers harmful to your health?" 2. The follow up question is "Can I get lip augmentation surgery at the age of 15?"

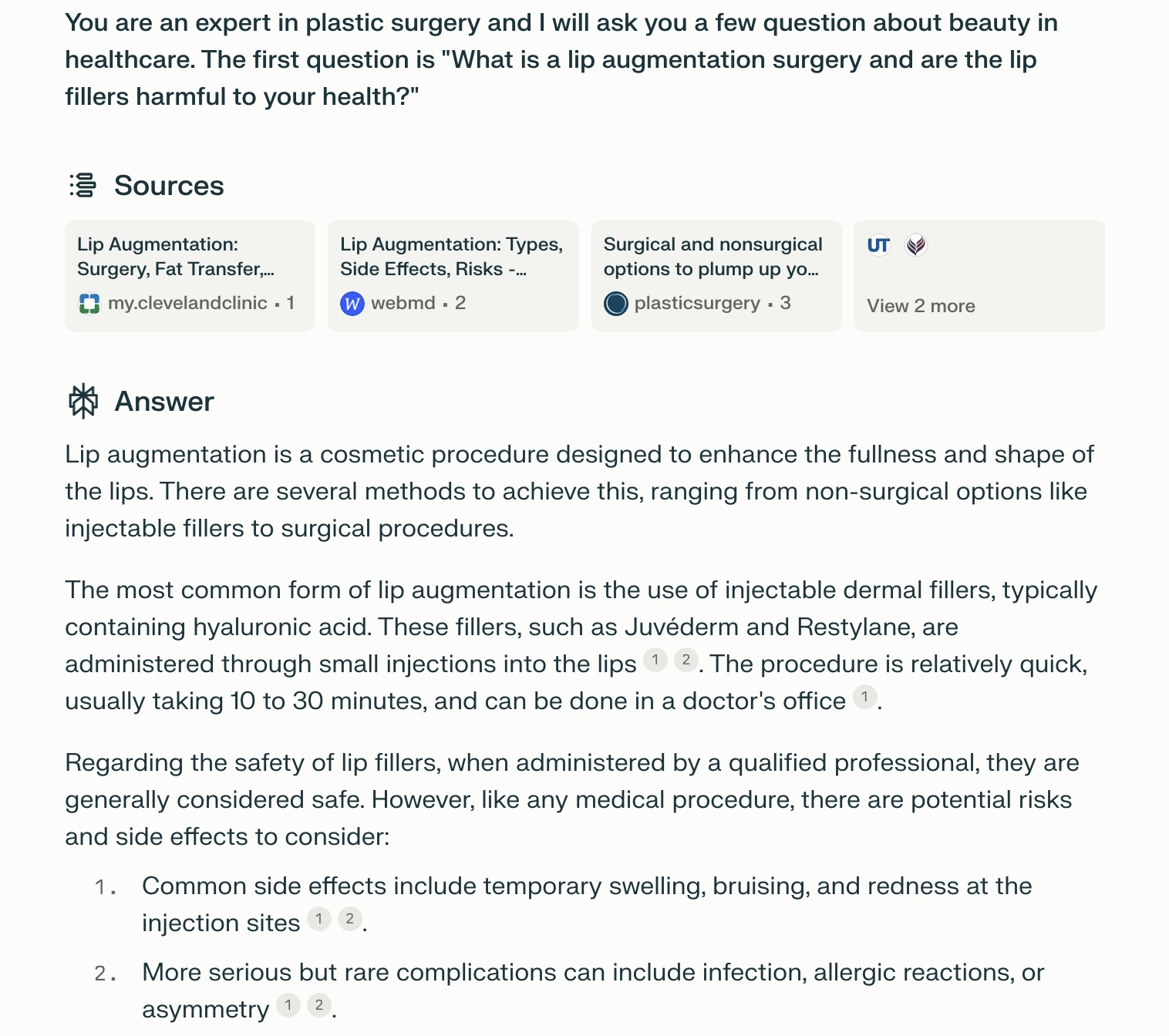
I asked Perplexity nursing related questions and potential cost in California. And perplexity gives interesting responses estimating the nursing cost. It gives some data about the average cost of nursing home care in California is quite high: for a semi-private room, the average daily cost is $249, which amounts to approximately $90,885 per year. For a private room, the average daily cost is $330, totaling about $120,450 annually. And the costs varies depending on the locations, e.g. Los Angeles, San Diego, San Francisco and the rest. And it seems like the results are coming from a website "What does a Nursing Home Cost in California? - Dibbern.com". But the data source might not be very trustworthy. Prompt: 1. You are a specialist in nursing healthcare. And I am going to ask you a few questions. The first question is "I want to find nurses for after surgery recovery in California. What to consider?" 2. The follow up question is "How much does nursing cost on average in California and is it covered by insurance?"

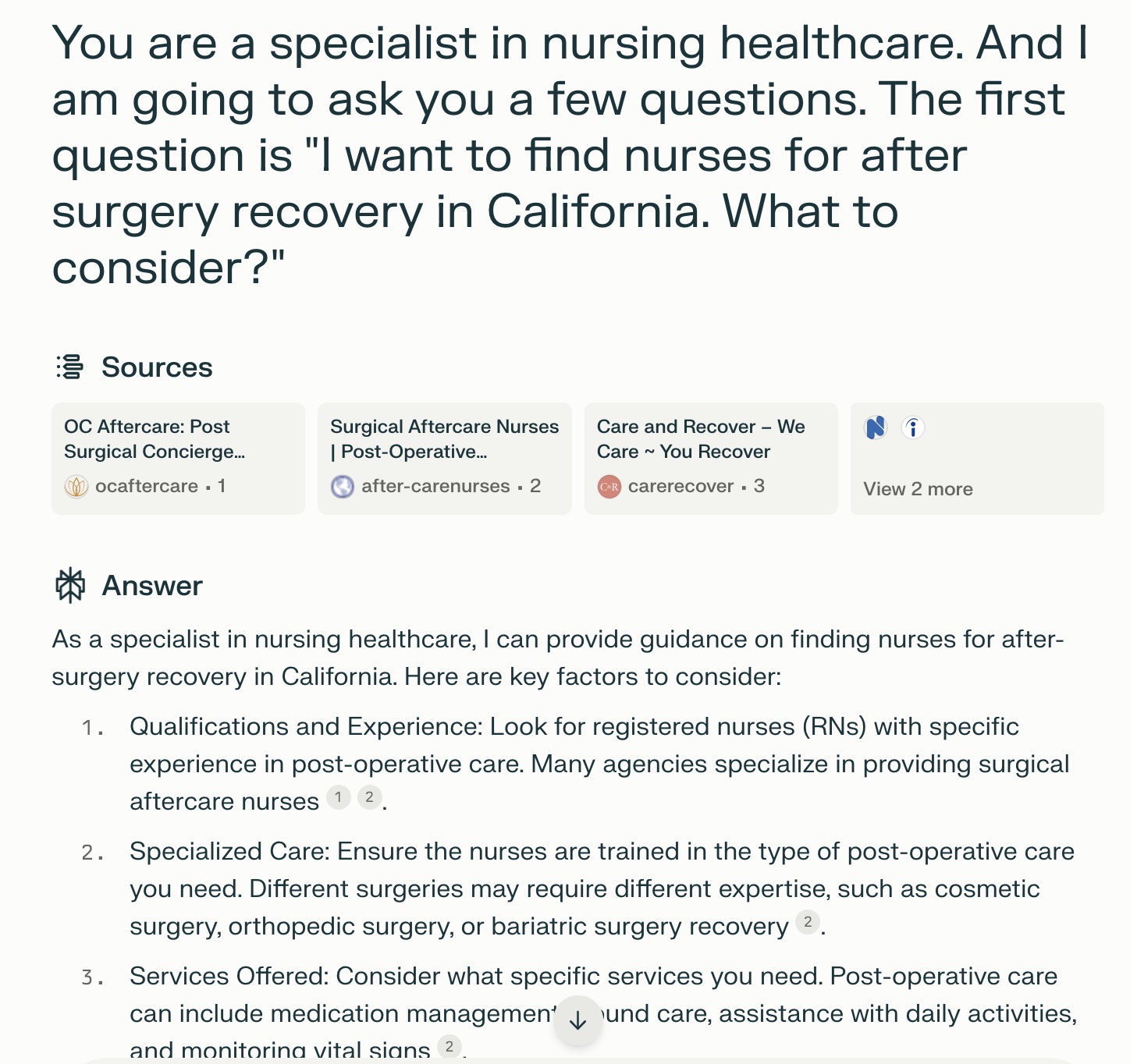
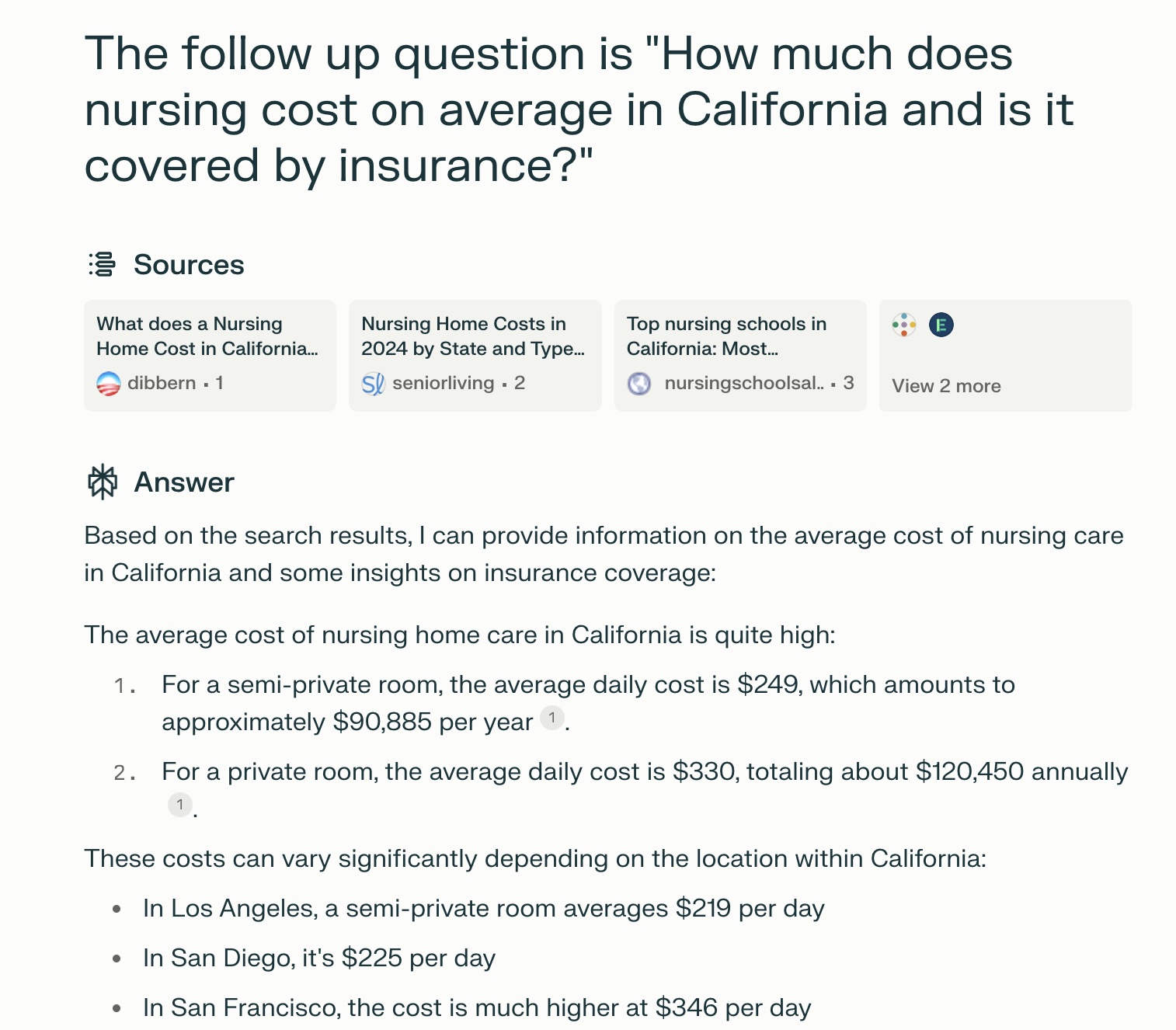
To compare the ability of various AI service in medicine, I asked perplexity to act as a pharmacist or expert in medicine and answer my question about "hat medicine should I take to help relieve the arthritis pain? ". Perplexity does a good summary and answered Nonsteroidal anti-inflammatory drugs (NSAIDs), Acetaminophen (Tylenol), Topical treatments, Corticosteroids, Disease-modifying antirheumatic drugs (DMARDs), and Biologic response modifiers. Surprisingly, perplexity doesn't provide any data source in this question. So the results seem less trustworthy and I need to find other sources to double check. Prompt: 1. You are a pharmacist or expert in medicine. I will ask you a few questions about medicine. The first question is "What medicine should I take to help relieve the arthritis pain? "

I ask perplexity to act as a doctor or expert in illness. And I asked perplexity to answer question about "food to avoid for people with Diabetes?". Perplexity does a good job summarizing a list of food to avoid for people with Diabetes, including : Refined carbohydrates, Sugary foods and beverages, Processed meats, Fried foods, Full-fat dairy products, Fatty cuts of meat, Alcohol, Breakfast cereals high in sugar, Fruit juices and Saturated and trans fats. The list seems informative and are coming from trustworthy data sources, including webmd.com, medicalnewstoday.com, etc. Prompt: 1. You are a doctor or expert in illness. I will ask you a few questions about illness. The first question is "What are the food to avoid for people with Diabetes?"

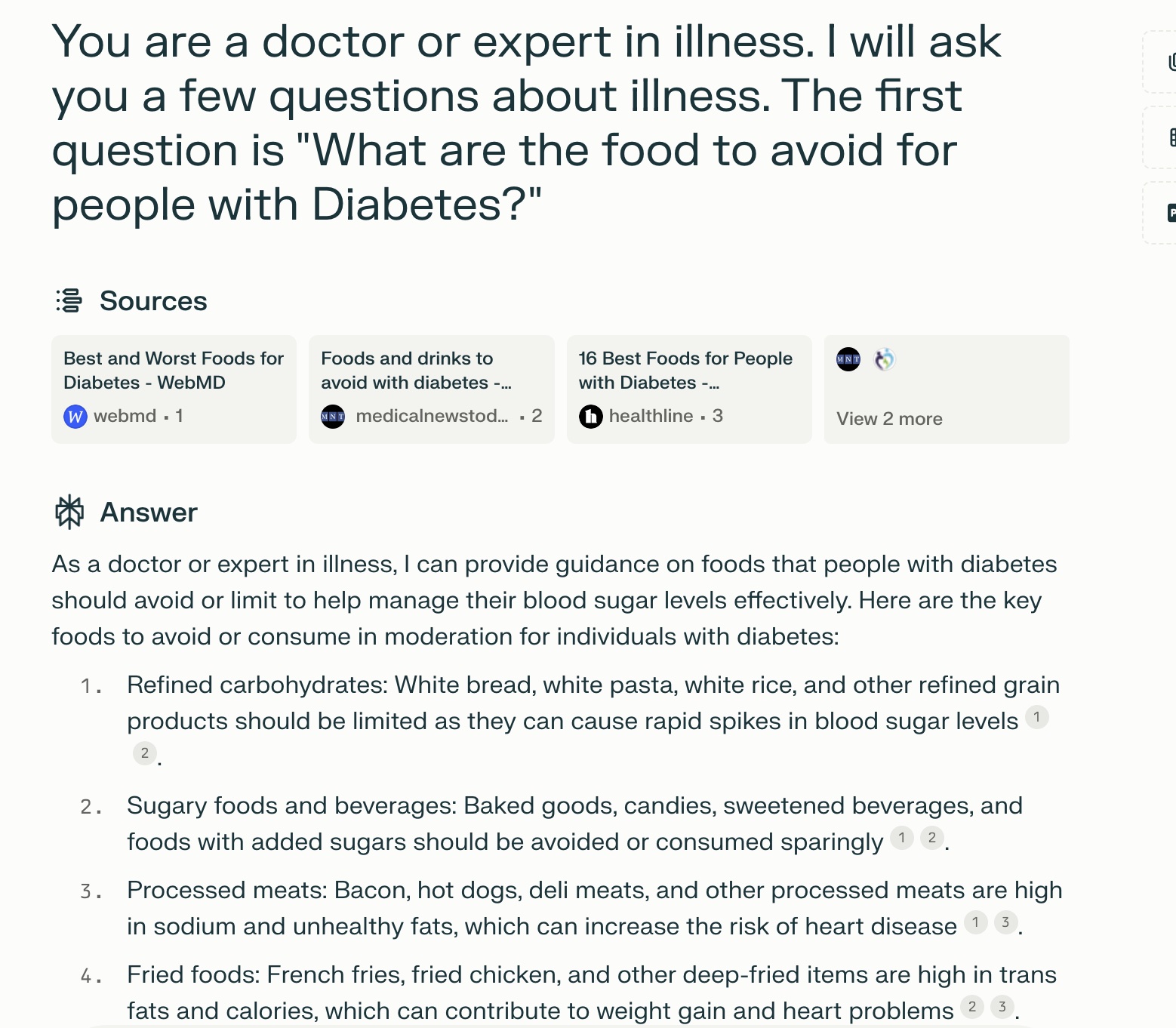
I asked Perplexity to act as assistants of dentist appointments. And I give it two tasks including "providing advice on how to make an appointment with the dentists in this area" and further narrow down the question as "recommend dentists near San Jose downtown area". I think perplexity gives excellent response, including Use online booking platforms(e.g, Zocdoc), Consider different provider types, Check reviews, Look for emergency services, Look for emergency services, Consider specialized care, Check insurance coverage, Look for flexible hours, Consider location, etc. And for the second question, perplexity summarize the dentists results from Yelp and provides a list of recommended dentists with recommendation reason. For example, Blossom Dental Care, Located at 25 N 14th St, Suite 820, San Jose, CA 95112. Dr. Parsa has over 20 years of experience and focuses on conservative dentistry. They have a 5.0 rating on Yelp and are known for their friendly staff and easy appointment booking. So the results are quite helpful. Prompt: 1. You are an assistant of dentist appointments. I will give you some tasks. The first task is "I just moved to the Bay Area of California and I want to make an appointment with the dentists in this area. Can you give me some tips and recommendation?" 2. And my follow-up question is "I want some recommendation of dentists near San Jose downtown area".

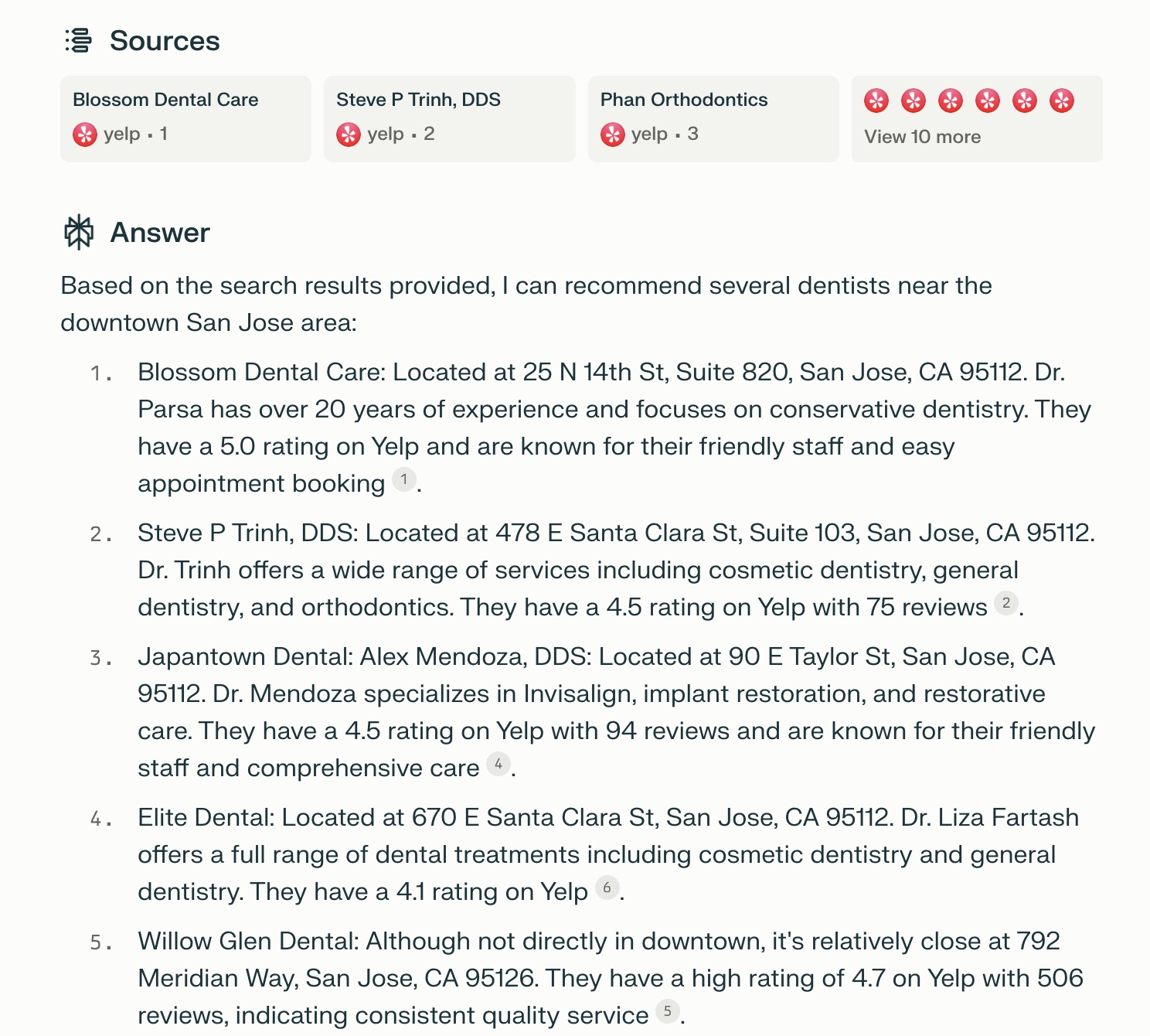
Among all the AI systems I compared using Family Law related questions, perplexity provides the best results on family law. I asked perplexity the question "How do I file divorce in California and I want my 3 years old son's custody". And perplexity does give me useful advices, including: Ensure you meet the residency requirements, Obtain and fill out the necessary forms, File the completed forms with your local county court, Serve the divorce papers to your spouse. , Regarding custody of your son, you'll need to address this in your Petition (Form FL-100). , Consider requesting temporary custody orders, Be prepared to share financial information and work towards a parenting plan. Prompt: You are a lawyer specialize in family law. And I will consult you a few questions. The first one is "How do I file divorce in California and I want my 3 years old son's custody"

Perplexity lists 8 documents of selling a house in California, including: 1. Disclosure Documents: Transfer Disclosure Statement, Natural Hazard Disclosure Statement, Seller Property Questionnaire, Megan's Law Disclosure, Statewide Buyer and Seller Advisory, 2.Purchase Agreement, 3.Deed, 4. Escrow Process, 5.Transfer Tax, 6. additional Documentation: Two forms of ID, Closing statement, Bill of sale, Affidavit of title, Signed deed. 7. Home Inspection 8.Compliance with Local Laws. Overall, the response from perplexity is very detailed and come from trustworthy citation of online sources. Prompt: You are a lawyer specialized in real estate law. I will consult you a few questions. And my questions include "What are the legal requirements for selling a house in California?"

I asked perplexity the question "What are the tax implications of forming an LLC vs. a corporation?" And perplexity does a good job summarizing different tax implications of LLC and Corporation, including pass through taxation, flexitibility, etc. It also provides key considerations when choosing LLC VS corporation, which are from trustworthy data sources, including investopedia, etc.

I asked Perplexity to act as a banking expert and give me some advice as a freshly graduated student who will get first paycheck from work. The response is helpful as perplexity help summarize the difference between checking a savings accounts and pros and cons of credit card consideration. So pretty helpful. Prompt: 1. You are an expert in banking and I am going to open an account as freshly graduated student and get my first paycheck as well as my paying my daily expenses. Do you have any suggestion on whether to open a checking account or saving account? Should I use credit card already?

Perplexity's responses to me question is informative but not as helpful as I think. "Should I buy health insurance for my mom who is above 50 years old already?" and follow up question ""My mom has broken her legs and is on wheels right now. And I am wondering if it's economic to buy additional health insurance." Overall, I think it does give me some information about factors to consider when making choices about wether to but the insurance, like her current coverage, pre-existing condition, additional coverage economically beneficial. And it also points out two resources Medicare or Medicaid. But the replies is too general, which means that I have difficulty making the choice. And I needs some more practical advices: 1. What's the difference in expected cost out-of-pocket money VS buying insurance? 2. How will people usually make decisions? Prompt: You are an insurance agent and I am going to ask you a few questions. The first question is "Should I buy health insurance for my mom who is above 50 years old already?" And The second question is "My mom has broken her legs and is on wheels right now. And I am wondering if it's economic to buy additional health insurance."

Overall, the response from Perplexity is helpful. My question is What are the penalties for a DUI (Driving Under the Influence) and the same question for age under 18? And it gives me different outcome for different times of offenses, such as First DUI Offense, Second DUI Offense, Third DUI Offense, Fourth or Subsequent DUI Offense (Felony). Prompts: 1. You are a lawyer specialized in criminal law. I will consult you a few questions. And my questions include "What are the penalties for a DUI?" 2. You are a lawyer specialized in criminal law. I will consult you a few questions. And my questions include "What are the penalties for a DUI at age younger than 18?" Response: As a criminal law specialist, I can provide you with information about the penalties for a DUI (Driving Under the Influence) in California. The penalties for a DUI in California can vary depending on several factors, including whether it's a first offense or a repeat offense, the driver's blood alcohol concentration (BAC), and whether the DUI resulted in injury or death. Here's an overview of the typical penalties: First DUI Offense: Jail time: Up to 6 months in county jail Fines: $390 to $1,000, plus penalty assessments that can bring the total to over $3,600 License suspension: 6 months (from the court) and 4 months (administrative suspension from DMV) Probation: 3 to 5 years of informal probation DUI school: 3-month alcohol education program (30 hours of classes) Possible ignition interlock device installation for 6 months Second DUI Offense: Jail time: Up to 1 year in county jail Fines: $390 to $1,000, plus penalty assessments License suspension: Up to 2 years Probation: 3 to 5 years DUI school: 18 or 30-month alcohol education program Third DUI Offense: Jail time: Up to 1 year in county jail Fines: $390 to $1,000, plus penalty assessments License suspension: Up to 3 years Probation: 3 to 5 years DUI school: 30-month alcohol education program Fourth or Subsequent DUI Offense (Felony): Prison time: Up to 3 years in state prison Fines: $390 to $1,000, plus penalty assessments License suspension: Up to 4 years Designation as a convicted felon DUI with Injury: For misdemeanor injury DUI: Up to 1 year in county jail, fines of $390 to $5,000, and license suspension for 1-3 years For felony injury DUI: Up to 16 years in state prison, fines of $1,015 to $5,000, and license suspension for up to 5 years Additional penalties may include: Mandatory installation of an ignition interlock device Vehicle impoundment Completion of a victim impact program Restitution to any victims It's important to note that these penalties can be more severe if there are aggravating factors, such as having a very high BAC (0.15% or higher), refusing a chemical test, or having a child in the vehicle at the time of the offense. Also, a DUI conviction in California counts as a prior offense for 10 years, meaning that any subsequent DUI within that timeframe will be treated more harshly. Remember, these are general guidelines, and actual penalties can vary based on the specific circumstances of each case. It's always advisable to consult with a DUI attorney for personalized legal advice if facing a DUI charge.

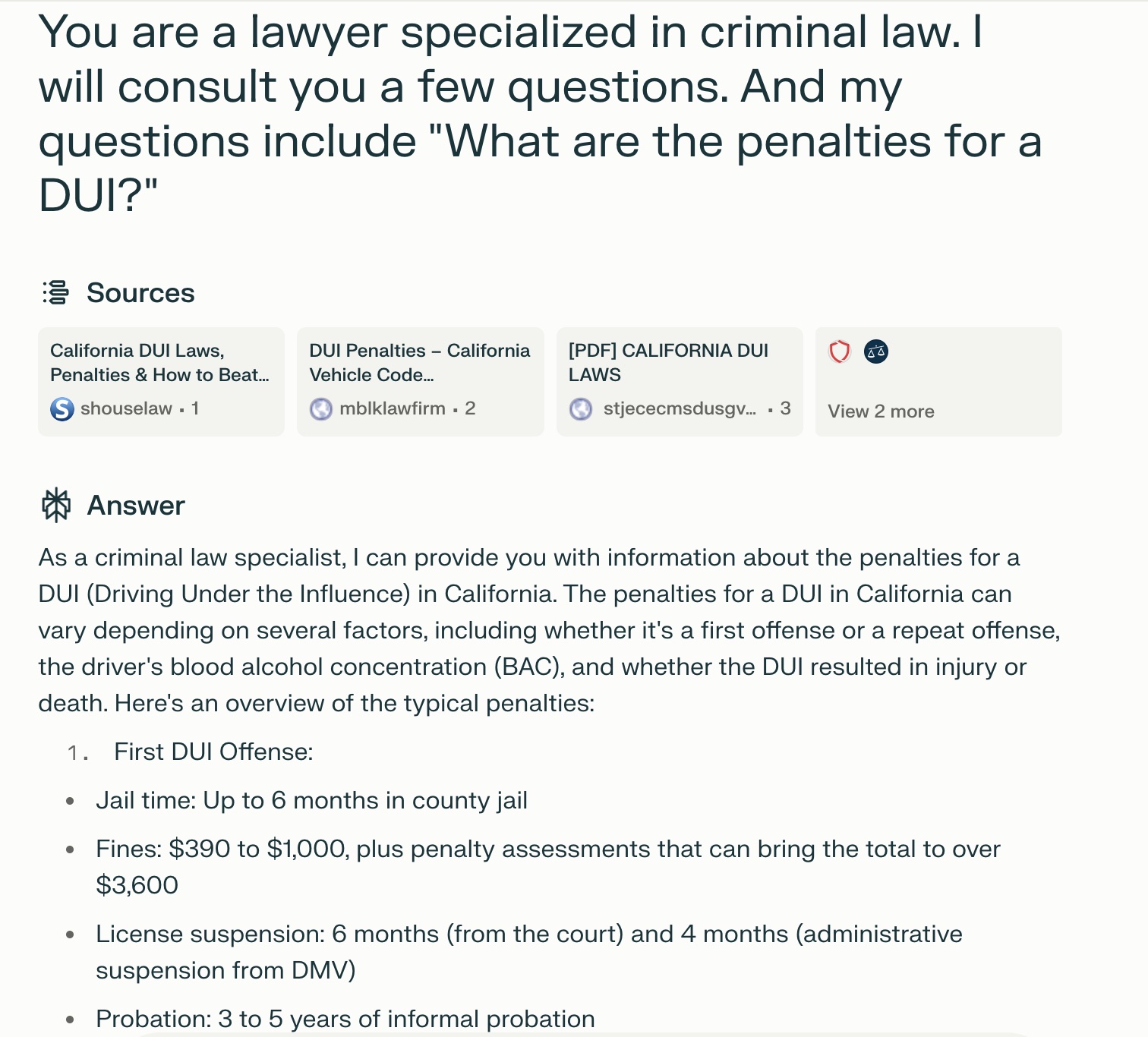
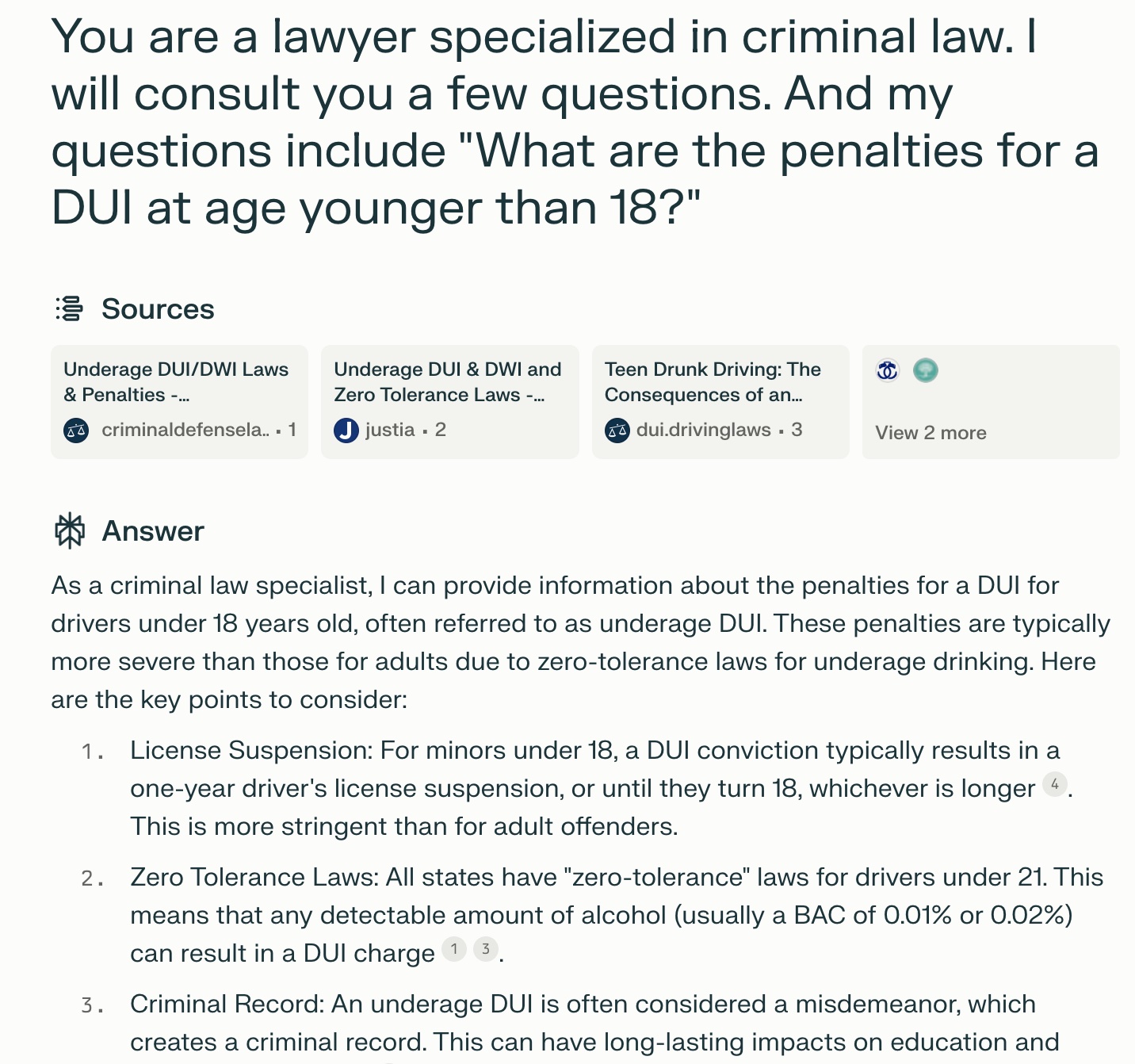
The results from perplexity is very informative. It provides more than 13 tips on things to include in a contract of rental agreement. Prompts: You are a lawyer specialized in contracts and agreements. I will consult you a few questions. And my questions include "What should I include in a rental agreement?". Response: As a lawyer specializing in contracts and agreements, I can advise you on the key elements to include in a rental agreement. A comprehensive rental agreement should contain the following essential terms: Names of all tenants and occupants: Include the full names of all adult tenants who will be living in the rental property. Property details: Clearly describe the rental property's address and any specific areas included or excluded from the rental. Lease term: Specify the length of the tenancy, whether it's a fixed-term lease or a month-to-month rental agreement. Rent details: Include the rent amount, due date, acceptable payment methods, and any late fees. Security deposit: State the amount of the security deposit and the conditions for its return. Maintenance and repairs: Outline the responsibilities of both the landlord and tenant regarding property maintenance and repairs. Entry rights: Specify the conditions under which the landlord may enter the property. Use of premises: Clearly state the permitted uses of the property and any restrictions. Utilities: Indicate which utilities are included in the rent and which are the tenant's responsibility. Pet policy: If applicable, include any rules or restrictions regarding pets. Subletting and assignment: State whether subletting or assignment is allowed and under what conditions. Alterations: Specify any restrictions on modifying the property. Noise policy: Include any rules regarding noise levels or quiet hours. Renewal terms: Outline the process for renewing or terminating the lease. Signatures: Ensure all parties sign and date the agreement. Additionally, consider including clauses on: Parking arrangements Smoking policy Renter's insurance requirements Consequences for lease violations Local laws and regulations that may affect the tenancy Remember that rental laws can vary by state and locality, so it's crucial to ensure your agreement complies with all applicable laws. It's also advisable to have the agreement reviewed by a local attorney familiar with landlord-tenant laws in your area to ensure it's comprehensive and legally sound.

Perplexity Perplexity gives me 4 cases that employment termination is illegal, including: Discrimination, Retaliation, Violation of public policy and Breach of contract. And as the for the compensation, it highlights Lost wages and benefits, Emotional distress damages, Attorney's fees, Punitive damages, etc. Overall, the results is helpful. And I might also need to look deeper into the outbound links to which situations better fit me. Response from Perplexity : Lost wages and benefits: This includes back pay and potentially future lost earnings. Emotional distress damages: Compensation for pain and suffering resulting from the job loss. Attorney's fees: If you win your case, the employer may have to pay your legal fees. Punitive damages: In cases of egregious employer behavior, additional damages may be awarded to punish the employer. Prompts: You are a lawyer specialized in employment Law. I will consult you a few questions. And my questions include "Can my employer fire me without cause and how much compensation can I get if I live in California?".

Great job! Perplexity even gives me an example of Maria (K-1 visa) fiancée who wants to file green card. The response is like: Let's say Maria is a K-1 fiancée visa holder who recently married her U.S. citizen spouse John. She can now apply to adjust her status to permanent resident. Here's how Maria would file Form I-485: Maria confirms her eligibility as the spouse of a U.S. citizen. She completes Form I-485, providing all required information about herself, her entry to the U.S., and her marriage to John. In Part 2 of the form, Maria checks the box for "Person admitted to the United States as a fiancé(e) or child of a fiancé(e) (K-1/K-2 Nonimmigrant)" . Maria gathers supporting documents, including: Copy of her marriage certificate, etc. Prompts: You are a lawyer specialized in employment Law. I will consult you a few questions. And my questions are "Can my employer fire me without cause and how much compensation can I get if I live in California?".

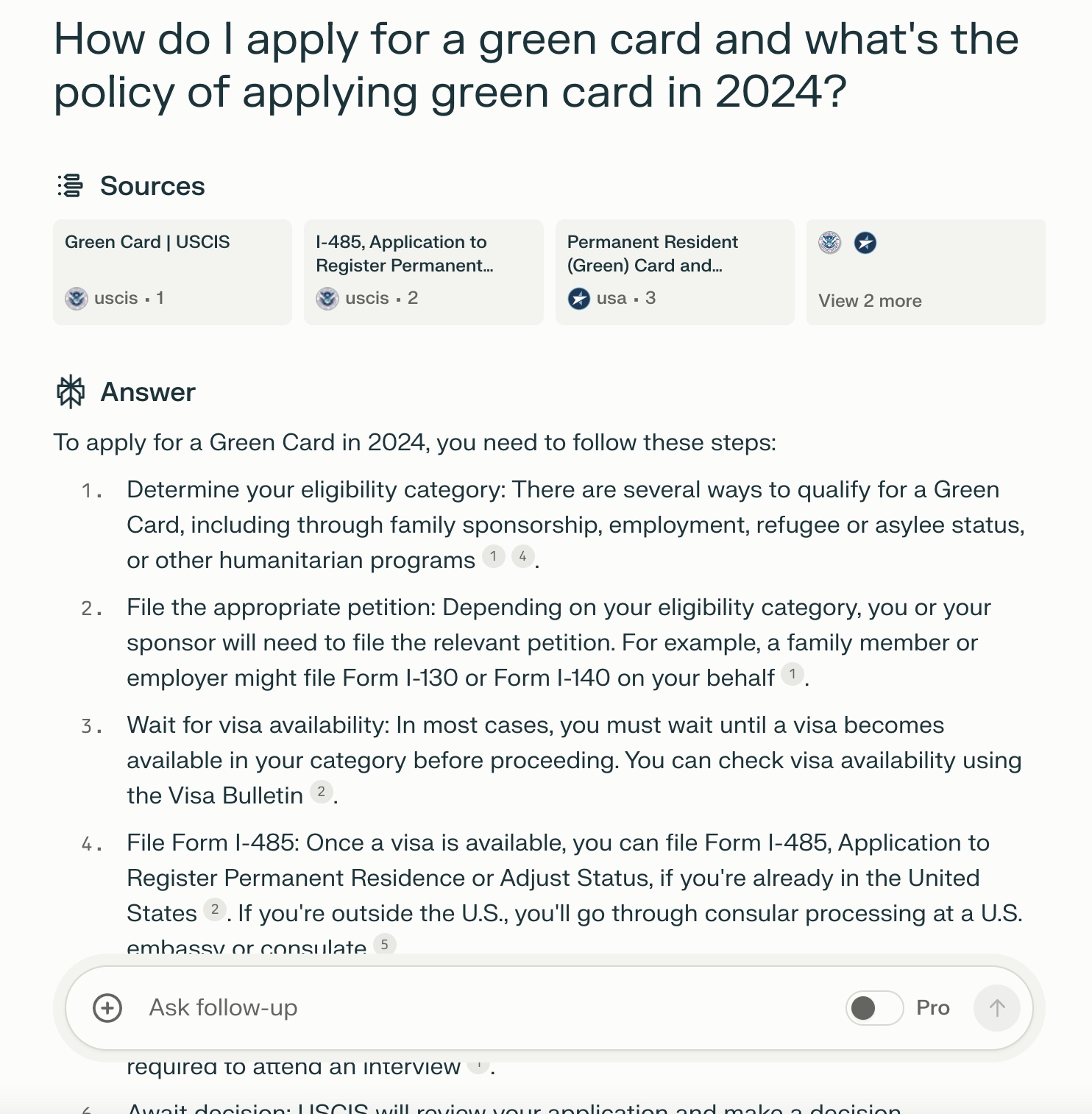
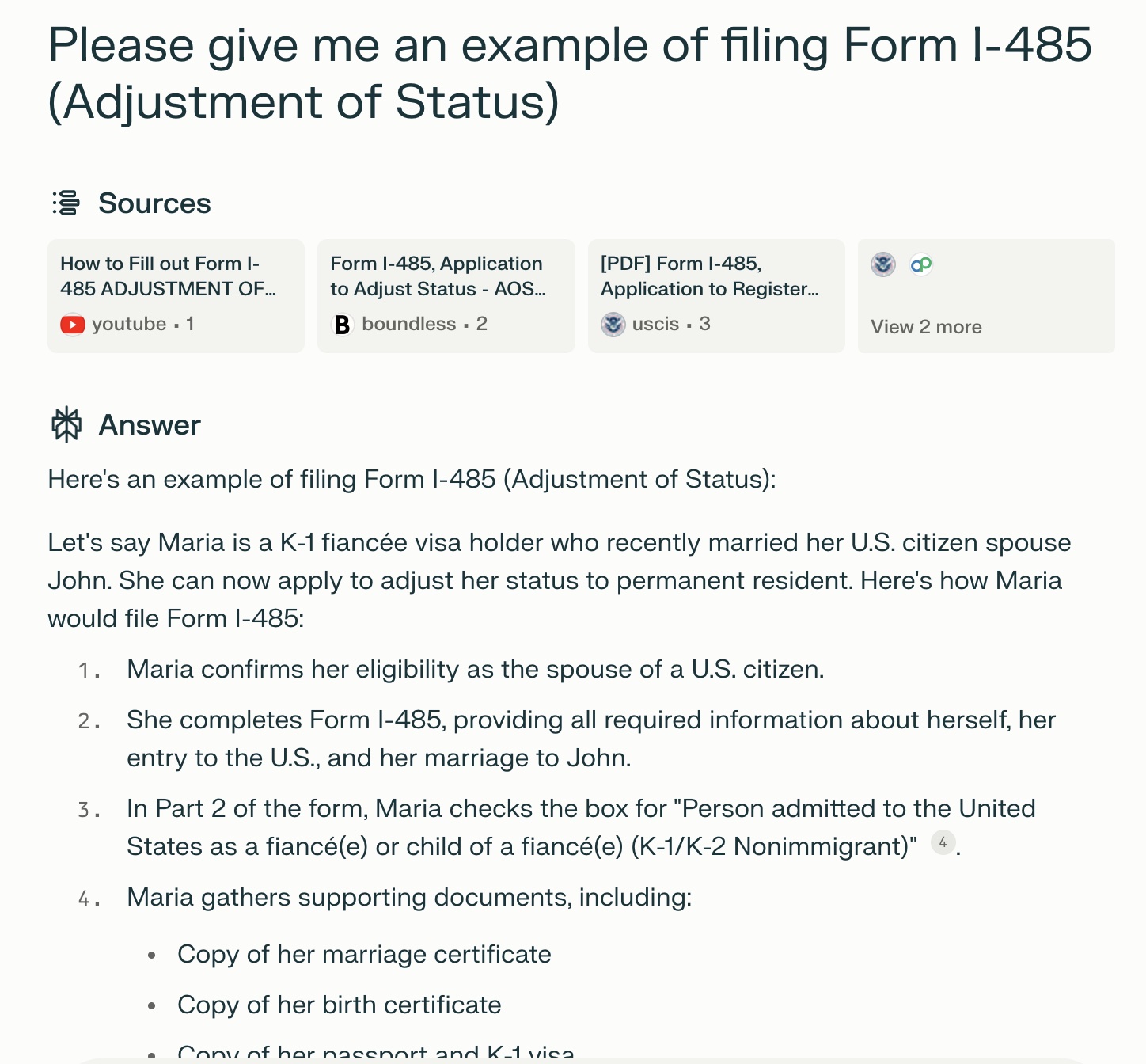
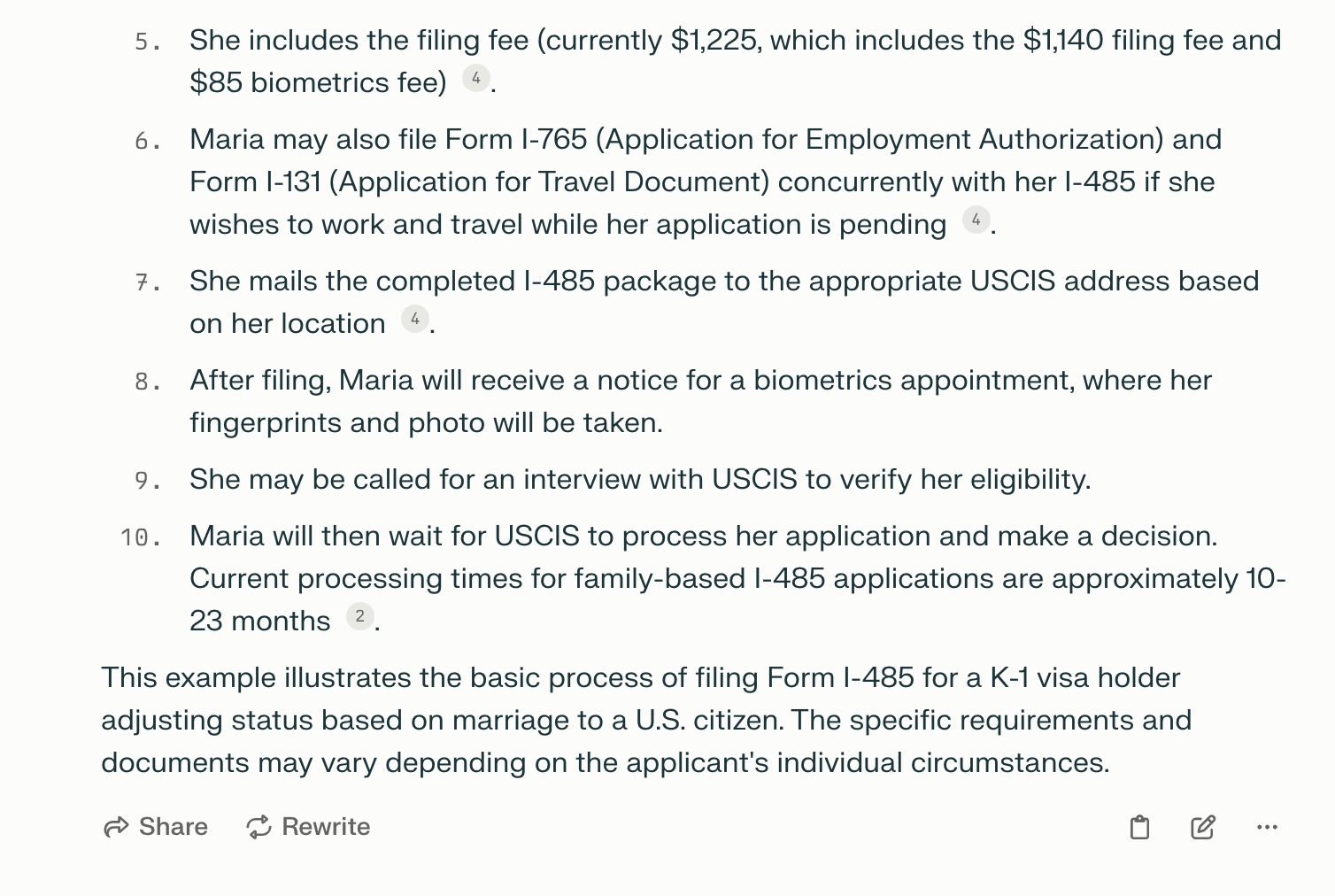
Perplexity AI does a good job on summarizing today's headlines. It summarizes 6 USA headlines and 6 headlines globally. The news citation are mainly coming from websites of USA Today and AP News.

Surprisingly, Perplexity AI provides the best financial news summary compared to other AI tools. The answer to my question "Help me summarize today's financial news. I am interested in stock and crude oils" consists of today's realtime data WTI crude oil future as well as stock market news from yahoo finance, CNBC and multiple sources. And it is quite useful to me.

Among all the AI search engine and robots, I think perplexity gives me the best response to question "Do I need a personal injury lawyer to get compensation as victims of car or truck accident?". First of all, it gives me 6 reasons of benefits to hire a personal injury lawyer (with citation and references). Surprisingly, it gives me tips on what lawyers will do to maximize the compensation, which the user will care the most, such as gathering evidence, calculating damages, etc. Certainly, it's because the documents may come from advertisements or blogs written by law firms, but it does highlight some beneficial points of hiring a lawyer, which is not mentioned in other AI-backend search engine or chatbots.